Page 161 - Aircraft Stuctures for Engineering Student

5.6 Energy method for the bending of thin plates 145

a'

T
z
(b)
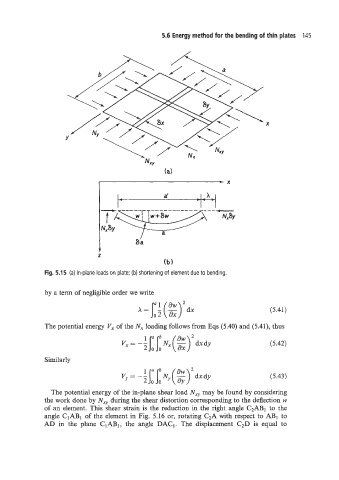
Fig. 5.1 5 (a) In-plane loads on plate; (b) shortening of element due to bending.

by a term of negligible order we write
A=/:-(-) 1 dw = dx (5.41)
2 8x
The potential energy V, of the N, loading follows from Eqs (5.40) and (5.41), thus
)
V, = - 1 r N, (g dxdy (5.42)
200
Similarly

(5.43)

The potential energy of the in-plane shear load Nxv may be found by considering
the work done by N.yy during the shear distortion corresponding to the deflection w
of an element. This shear strain is the reduction in the right angle C2ABl to the
angle CIABl of the element in Fig. 5.16 or, rotating C2A with respect to AB, to
AD in the plane CIAB1, the angle DACl. The displacement C2D is equal to