Page 89 - Aircraft Stuctures for Engineering Student

74 Energy methods of structural analysis

is then

2 PrSAr
r= 1
This work will be accompanied by an increment of strain energy SU in the elastic body
since by specifying virtual displacements of the loads we automatically impose virtual
displacements on the particles of the body itself, as the body is continuous and is
assumed to remain so. This increment in strain energy may be regarded as negative
virtual work done by the particles so that the total work done during the virtual
displacement is
n
-SU i- PrSAr
r=l
The body is in equilibrium under the applied loads so that by the principle of virtual
work the above expression must be equal to zero. Hence
n
SU - PJA, = 0 (4.10)
r=l
The loads Pr remain constant during the virtual displacement; therefore, Eq. (4.10)
may be written
n
SU - S P,Ar = 0
r=l
or, from Eq. (4.6)
S(U+ V) = 0 (4.11)
Thus, the total potential energy of an elastic system has a stationary value for all small
displacements if the system is in equilibrium. It may also be shown that if the
stationary value is a minimum the equilibrium is stable. A qualitative demonstration
of this fact is sacient for our purposes, although mathematical proofs exist'. In
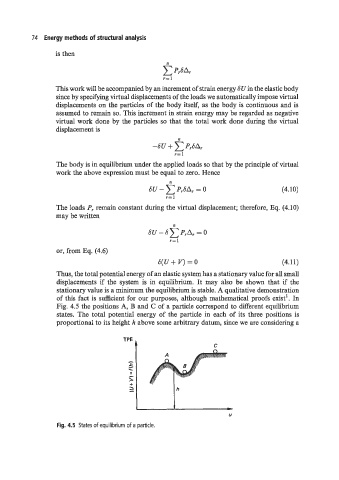
Fig. 4.5 the positions A, B and C of a particle correspond to different equilibrium
states. The total potential energy of the particle in each of its three positions is
proportional to its height h above some arbitrary datum, since we are considering a

Fig. 4.5 States of equilibrium of a particle.