Page 62 -

42 CHAPTER 2 AN INTRODUCTION TO LINEAR PROGRAMMING

Recall that the inequality representing the cutting and dyeing constraint is:
0:7S þ 1D 630
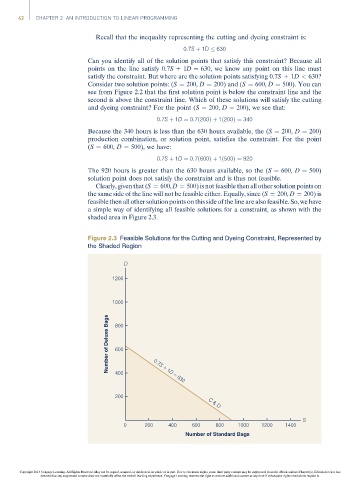
Can you identify all of the solution points that satisfy this constraint? Because all
points on the line satisfy 0.7S +1D ¼ 630, we know any point on this line must
satisfy the constraint. But where are the solution points satisfying 0.7S +1D < 630?
Consider two solution points: (S ¼ 200, D ¼ 200) and (S ¼ 600, D ¼ 500). You can
see from Figure 2.2 that the first solution point is below the constraint line and the
second is above the constraint line. Which of these solutions will satisfy the cutting
and dyeing constraint? For the point (S ¼ 200, D ¼ 200), we see that:
0:7S þ 1D ¼ 0:7ð200Þþ 1ð200Þ¼ 340
Because the 340 hours is less than the 630 hours available, the (S ¼ 200, D ¼ 200)
production combination, or solution point, satisfies the constraint. For the point
(S ¼ 600, D ¼ 500), we have:
0:7S þ 1D ¼ 0:7ð600Þþ 1ð500Þ¼ 920

The 920 hours is greater than the 630 hours available, so the (S ¼ 600, D ¼ 500)
solution point does not satisfy the constraint and is thus not feasible.
Clearly, given that (S ¼ 600, D ¼ 500) is not feasible then all other solution points on
the same side of the line will not be feasible either. Equally, since (S ¼ 200, D ¼ 200) is
feasible then all other solution points on this side of the line are also feasible. So, we have
a simple way of identifying all feasible solutions for a constraint, as shown with the
shaded area in Figure 2.3.

Figure 2.3 Feasible Solutions for the Cutting and Dyeing Constraint, Represented by
the Shaded Region

D

1200

1000

Number of Deluxe Bags 800

600

400

200 0.7S + 1D = 630 C & D

S
0 200 400 600 800 1000 1200 1400
Number of Standard Bags

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.