Page 116 - Analog and Digital Filter Design

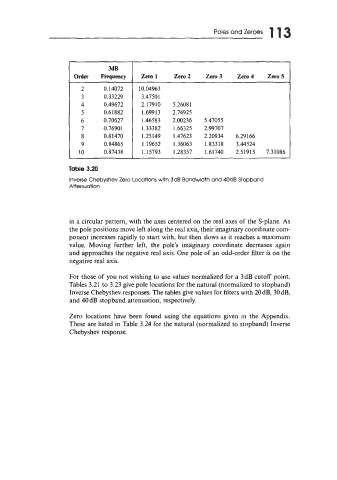
Poles andZeroes 1 1 3

I i
3dB
Freclueaey zen,l Zero2 Zero3 Zero4 Zero5
2 0.14072 10.04963
3 0.33229 3.47501
4 0.49672 2.17910 5.26081
5 0.6 1882 1.69913 2.74925
6 0.70627 1.46583 2.00236 5.47055
7 0.76901 1.33382 1.66325 2.99707
8 0.81470 1.25149 1.47623 2.20934 6.29166
9 0.84865 1.19652 1.36063 1.833 18 3.44524
10 0.87438 1.15793 1.28357 1.61740 2.51915 7.31086

TaMe 3.20
Inverse Chebyshev Zero Locations with 3dB Bandwidth and 40dB Stopband
Attenuation

in a circular pattern, with the axes centered on the real axes of the S-plane. As
the pole positions move left along the real axis, their imaginary coordinate com-
ponent increases rapidly to start with, but then slows as it reaches a maximum
value. Moving further left, the pole’s imaginary coordinate decreases again
and approaches the negative real axis. One pole of an odd-order filter is on the
negative real axis.

For those of you not wishing to use values normalized for a 3dB cutoff point,
Tables 3.21 to 3.23 give pole locations for the natural (normalized to stopband)
Inverse Chebyshev responses. The tables give values for filters with 20dB, 30dB,
and 40dB stopband attenuation, respectively.

Zero locations have been found using the equations given in the Appendix.
These are listed in Table 3.24 for the natural (normalized to stopband) Inverse
Chebyshev response.