Page 187 - Analysis, Synthesis and Design of Chemical Processes, Third Edition

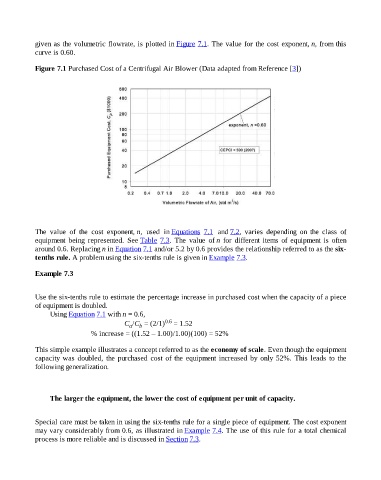
given as the volumetric flowrate, is plotted in Figure 7.1. The value for the cost exponent, n, from this
curve is 0.60.

Figure 7.1 Purchased Cost of a Centrifugal Air Blower (Data adapted from Reference [3])

The value of the cost exponent, n, used in Equations 7.1 and 7.2, varies depending on the class of
equipment being represented. See Table 7.3. The value of n for different items of equipment is often

around 0.6. Replacing n in Equation 7.1 and/or 5.2 by 0.6 provides the relationship referred to as the six-
tenths rule. A problem using the six-tenths rule is given in Example 7.3.

Example 7.3

Use the six-tenths rule to estimate the percentage increase in purchased cost when the capacity of a piece
of equipment is doubled.
Using Equation 7.1 with n = 0.6,
0.6
C /C = (2/1) = 1.52
b
a
% increase = ((1.52 – 1.00)/1.00)(100) = 52%

This simple example illustrates a concept referred to as the economy of scale. Even though the equipment
capacity was doubled, the purchased cost of the equipment increased by only 52%. This leads to the
following generalization.

The larger the equipment, the lower the cost of equipment per unit of capacity.

Special care must be taken in using the six-tenths rule for a single piece of equipment. The cost exponent
may vary considerably from 0.6, as illustrated in Example 7.4. The use of this rule for a total chemical
process is more reliable and is discussed in Section 7.3.