Page 372 - Applied Numerical Methods Using MATLAB

PROBLEMS 361
10

5

0

−5

−10
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
2
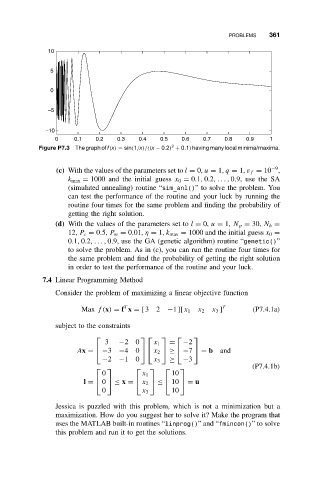
Figure P7.3 Thegraph off(x) = sin(1/x)/((x − 0.2) + 0.1) havingmanylocalminima/maxima.

−9
(c) With the values of the parameters set to l = 0, u = 1, q = 1, ε f = 10 ,
k max = 1000 and the initial guess x 0 = 0.1, 0.2,..., 0.9, use the SA
(simulated annealing) routine “sim_anl()” to solve the problem. You
can test the performance of the routine and your luck by running the
routine four times for the same problem and finding the probability of
getting the right solution.

(d) With the values of the parameters set to l = 0, u = 1, N p = 30, N b =
12, P c = 0.5, P m = 0.01, η = 1, k max = 1000 and the initial guess x 0 =
0.1, 0.2,. .., 0.9, use the GA (genetic algorithm) routine “genetic()”
to solve the problem. As in (c), you can run the routine four times for
the same problem and find the probability of getting the right solution
in order to test the performance of the routine and your luck.
7.4 Linear Programming Method
Consider the problem of maximizing a linear objective function

T
Max f(x) = f x = [ 32 −1 ][ x 1 x 2 x 3 ] T (P7.4.1a)
subject to the constraints

     
3 −20 x 1 = −2
Ax =  −3 −40   x 2  ≥  −7  = b and
−2 −10 x 3 ≥ −3
(P7.4.1b)
     
0 x 1 10
0
l =   ≤ x =  x 2  ≤  10  = u
0 x 3 10
Jessica is puzzled with this problem, which is not a minimization but a
maximization. How do you suggest her to solve it? Make the program that
uses the MATLAB built-in routines “linprog()”and “fmincon()” to solve
this problem and run it to get the solutions.