Page 122 - Applied Petroleum Geomechanics

114 Applied Petroleum Geomechanics

s 3 ¼ 50 MPa, and the hydrostatic pressure p n ¼ 31 MPa. Two scenarios on
how pore pressure variations impact the minimum stress are examined here.
If the total stresses (s 1 , s 2 , and s 3 ) keep unchanged with pore pressure
variations, the increase in pore pressure (or overpressure) will reduce the
0
0
minimum and maximum effective stresses (s 1 , s 3 ). This will move the
Mohr circle to the left side, making the Mohr circle touch or cross the shear
failure envelope and causing shear failures (Fig. 3.22A). However, in most
cases the increase of pore pressure may also cause the minimum horizontal
stress s 3 to increase as field observed (e.g., Hillis, 2000; Engelder and
Fischer, 1994). Therefore, the other scenario is that the increase in the
minimum horizontal stress induced by the increase of pore pressure causes
the Mohr circle size reduction (Fig. 3.22B) with assumption of no change in
vertical stress s V . The rock in this case is much less likely to have shear
failures than the one shown in Fig. 3.22A. By contrast, the decrease in pore
pressure (e.g., the reservoir depletion) increases the Mohr circle size and
moves the circle to the right side (Dohmen et al., 2013, 2017), and the
increased Mohr circle sizes may, then, cross the shear failure envelope and
cause shear failures (see Fig. 3.22B).

3.4.2.2 Modified MohreCoulomb failure criterion
Triaxial tests have found that the MohreCoulomb failure envelope has a
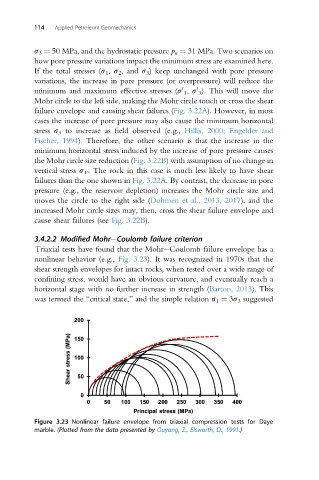
nonlinear behavior (e.g., Fig. 3.23). It was recognized in 1970s that the
shear strength envelopes for intact rocks, when tested over a wide range of
confining stress, would have an obvious curvature, and eventually reach a
horizontal stage with no further increase in strength (Barton, 2013). This
was termed the “critical state,” and the simple relation s 1 ¼ 3s 3 suggested

Figure 3.23 Nonlinear failure envelope from triaxial compression tests for Daye
marble. (Plotted from the data presented by Ouyang, Z., Elsworth, D., 1991.)