Page 196 - Applied Petroleum Geomechanics

In situ stress estimate 191

required to open a fracture is equal to the overburden gradient. When
combined with the contribution of the overlying sea water (Barker and
Woods suggested r w ¼ 8.55 ppg as the average density of sea water for
deepwater Gulf of Mexico wells), the following expression was presented:
1:1356
r Z w þ 5:3ðZ Z w Z ag Þ
w
OBG ¼ (6.7)
Z
where OBG is in ppg, water density is in ppg and the depth is in ft.
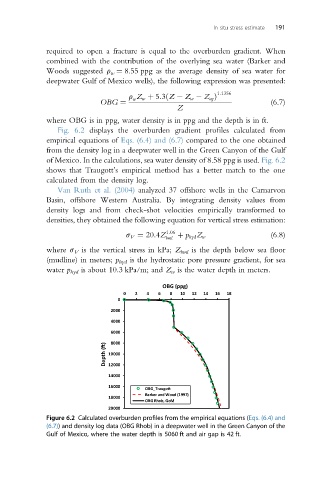
Fig. 6.2 displays the overburden gradient profiles calculated from
empirical equations of Eqs. (6.4) and (6.7) compared to the one obtained
from the density log in a deepwater well in the Green Canyon of the Gulf
of Mexico. In the calculations, sea water density of 8.58 ppg is used. Fig. 6.2
shows that Traugott’s empirical method has a better match to the one
calculated from the density log.
Van Ruth et al. (2004) analyzed 37 offshore wells in the Carnarvon
Basin, offshore Western Australia. By integrating density values from
density logs and from check-shot velocities empirically transformed to
densities, they obtained the following equation for vertical stress estimation:
s V ¼ 20:4Z 1:06 þ p hyd Z w (6.8)
bml
where s V is the vertical stress in kPa; Z bml is the depth below sea floor
(mudline) in meters; p hyd is the hydrostatic pore pressure gradient, for sea
water p hyd is about 10.3 kPa/m; and Z w is the water depth in meters.

OBG (ppg)
0 2 4 6 8 10 12 14 16 18
0
2000
4000
6000
8000
Depth ( ) 10000
12000
14000
16000
OBG_Traugo
Barker and Wood (1997)
18000
OBG Rhob, GoM
20000
Figure 6.2 Calculated overburden profiles from the empirical equations (Eqs. (6.4) and
(6.7)) and density log data (OBG Rhob) in a deepwater well in the Green Canyon of the
Gulf of Mexico, where the water depth is 5060 ft and air gap is 42 ft.