Page 221 - Applied Probability

10. Molecular Phylogeny 207

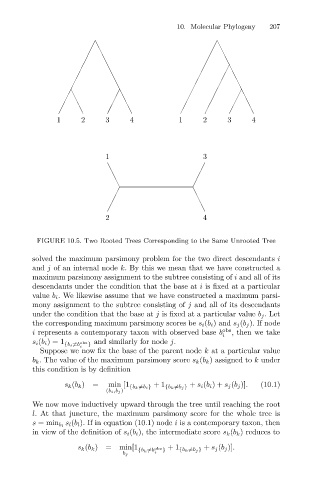
1 2 3 4 1 2 3 4
1 3

2 4
FIGURE 10.5. Two Rooted Trees Corresponding to the Same Unrooted Tree
solved the maximum parsimony problem for the two direct descendants i
and j of an internal node k. By this we mean that we have constructed a
maximum parsimony assignment to the subtree consisting of i and all of its
descendants under the condition that the base at i is fixed at a particular
value b i . We likewise assume that we have constructed a maximum parsi-
mony assignment to the subtree consisting of j and all of its descendants
under the condition that the base at j is fixed at a particular value b j . Let
the corresponding maximum parsimony scores be s i (b i ) and s j (b j ). If node
i represents a contemporary taxon with observed base b obs , then we take
i
s i (b i )=1 {b i =b obs and similarly for node j.
}
i
Suppose we now fix the base of the parent node k at a particular value
b k . The value of the maximum parsimony score s k (b k ) assigned to k under
this condition is by definition
s k (b k ) = min [1 {b k =b i } +1 {b k =b j } + s i (b i )+ s j (b j )]. (10.1)
(b i ,b j )

We now move inductively upward through the tree until reaching the root
l. At that juncture, the maximum parsimony score for the whole tree is
s l (b l ). If in equation (10.1) node i is a contemporary taxon, then
s =min b l
in view of the definition of s i (b i ), the intermediate score s k (b k ) reduces to
s k (b k )=min[1 {b k =b obs +1 {b k =b j } + s j (b j )].
}
b j i