Page 353 - Applied Statistics And Probability For Engineers

c09.qxd 5/15/02 8:02 PM Page 301 RK UL 9 RK UL 9:Desktop Folder:

9-3 TESTS ON THE MEAN OF A NORMAL DISTRIBUTION, VARIANCE UNKNOWN 301

normal. The important result upon which the test procedure relies is that if X , X , p , X is a
1
n
2
2
random sample from a normal distribution with mean and variance , the random variable
X
T
S
1n
has a t distribution with n
1 degrees of freedom. Recall that we used this result in Section
8-3 to devise the t-confidence interval for . Now consider testing the hypotheses

H : 0
0
H : 0
1
We will use the test statistic
X
0
T (9-23)
0
S
1n
If the null hypothesis is true, T 0 has a t distribution with n
1 degrees of freedom. When we
know the distribution of the test statistic when H 0 is true (this is often called the reference
distribution or the null distribution), we can locate the critical region to control the type I
error probability at the desired level. In this case we would use the t percentage points
t 2,n
1
and t
2,n
1 as the boundaries of the critical region so that we would reject H 0 : 0 if
t t
2,n
1 or if t
t
2,n
1
0
0
where t 0 is the observed value of the test statistic T 0 . The test procedure is very similar to the
test on the mean with known variance described in Section 9-2, except that T 0 is used as the
test statistic instead of Z 0 and the t n
1 distribution is used to define the critical region instead
of the standard normal distribution. A summary of the test procedures for both two- and one-
sided alternative hypotheses follows:
The One-
Sample t-Test Null hypothesis: H 0 : 0

X
0
Test statistic: T
0
S
1n
Alternative hypothesis Rejection criteria
H 1 : Z 0 t 0 t /2,n
1 or t 0
t /2,n
1
H 1 : 0 t 0 t ,n
1
H 1 : 0 t 0
t ,n
1

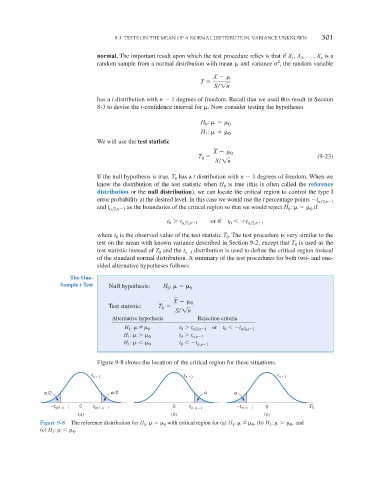
Figure 9-8 shows the location of the critical region for these situations.

t n – 1 t n – 1 t n – 1

α
/2
/2 α α α
–t α 0 t α 0 t α –t α 0 T 0
, n – 1
/2, n – 1
, n – 1
/2, n – 1
(a) (b) (c)
Figure 9-8 The reference distribution for H 0 : 0 with critical region for (a) H 1 : Z 0 , (b) H 1 : 0 , and
(c) H 1 : 0 .