Page 51 - Applied Statistics And Probability For Engineers

c02.qxd 5/10/02 1:07 PM Page 34 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

34 CHAPTER 2 PROBABILITY

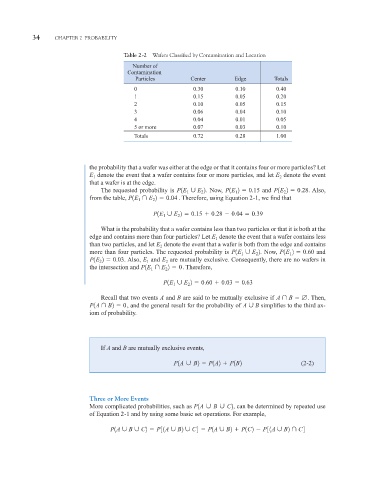
Table 2-2 Wafers Classified by Contamination and Location
Number of
Contamination
Particles Center Edge Totals
0 0.30 0.10 0.40
1 0.15 0.05 0.20
2 0.10 0.05 0.15
3 0.06 0.04 0.10
4 0.04 0.01 0.05
5 or more 0.07 0.03 0.10
Totals 0.72 0.28 1.00

the probability that a wafer was either at the edge or that it contains four or more particles? Let
E denote the event that a wafer contains four or more particles, and let E 2 denote the event
1
that a wafer is at the edge.
The requested probability is P1E ´ E 2 . Now, P1E 2 0.15 and P1E 2 0.28 . Also,
1
2
1
2
from the table, P1E ¨ E 2 0.04 . Therefore, using Equation 2-1, we find that
2
1
P1E ´ E 2 0.15 0.28 0.04 0.39
1
2
What is the probability that a wafer contains less than two particles or that it is both at the
denote the event that a wafer contains less
edge and contains more than four particles? Let E 1
than two particles, and let E denote the event that a wafer is both from the edge and contains
2
more than four particles. The requested probability is P1E ´ E 2 . Now, P1E 2 0.60 and
1
2
1
P1E 2 0.03 . Also, E and E are mutually exclusive. Consequently, there are no wafers in
2
2
1
the intersection and P1E ¨ E 2 0 . Therefore,
2
1
P1E ´ E 2 0.60 0.03 0.63
2
1
Recall that two events A and B are said to be mutually exclusive if A ¨ B . Then,
P1A ¨ B2 0 , and the general result for the probability of A ´ B simplifies to the third ax-
iom of probability.
If A and B are mutually exclusive events,
P1A ´ B2 P1A2 P1B2 (2-2)

Three or More Events
More complicated probabilities, such as P1A ´ B ´ C2 , can be determined by repeated use
of Equation 2-1 and by using some basic set operations. For example,

P1A ´ B ´ C2 P31A ´ B2 ´ C4 P1A ´ B2 P1C2 P31A ´ B2 ¨ C4