Page 55 - Applied Statistics And Probability For Engineers

c02.qxd 5/10/02 1:07 PM Page 38 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

38 CHAPTER 2 PROBABILITY

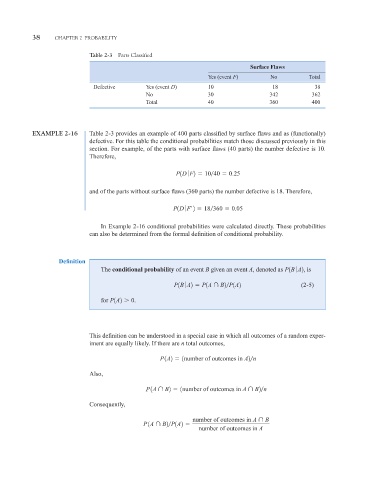
Table 2-3 Parts Classified
Surface Flaws
Yes (event F) No Total
Defective Yes (event D) 10 18 38
No 30 342 362
Total 40 360 400

EXAMPLE 2-16 Table 2-3 provides an example of 400 parts classified by surface flaws and as (functionally)
defective. For this table the conditional probabilities match those discussed previously in this
section. For example, of the parts with surface flaws (40 parts) the number defective is 10.
Therefore,

P1D ƒ F2 10
40 0.25

and of the parts without surface flaws (360 parts) the number defective is 18. Therefore,

P1D ƒ F¿2 18
360 0.05

In Example 2-16 conditional probabilities were calculated directly. These probabilities
can also be determined from the formal definition of conditional probability.

Definition
The conditional probability of an event B given an event A, denoted as P1B ƒ A2 , is

P1B ƒ A2 P1A ¨ B2
P1A2 (2-5)

for P1A2 0 .

This definition can be understood in a special case in which all outcomes of a random exper-
iment are equally likely. If there are n total outcomes,

P 1A2 1number of outcomes in A2
n

Also,

P 1A ¨ B2 1number of outcomes in A ¨ B2
n

Consequently,

number of outcomes in A ¨ B
P 1A ¨ B2
P1A2
number of outcomes in A