Page 54 - Applied Statistics And Probability For Engineers

c02.qxd 5/10/02 1:07 PM Page 37 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

2-4 CONDITIONAL PROBABILITY 37

Tool 1 (a) If a shaft is selected at random, what is the probability that
roundness conforms the shaft conforms to surface finish requirements or to
roundness requirements or is from Tool 1?
yes no
(b) If a shaft is selected at random, what is the probability that
surface finish yes 200 1
the shaft conforms to surface finish requirements or does
conforms no 4 2 not conform to roundness requirements or is from Tool 2?
Tool 2 (c) If a shaft is selected at random, what is the probability that
the shaft conforms to both surface finish and roundness
roundness conforms
requirements or the shaft is from Tool 2?
yes no (d) If a shaft is selected at random, what is the probability that
surface finish yes 145 4 the shaft conforms to surface finish requirements or the
conforms no 8 6 shaft is from Tool 2?

2-4 CONDITIONAL PROBABILITY

A digital communication channel has an error rate of one bit per every thousand transmitted.
Errors are rare, but when they occur, they tend to occur in bursts that affect many consecutive
bits. If a single bit is transmitted, we might model the probability of an error as 1 1000.
However, if the previous bit was in error, because of the bursts, we might believe that the
probability that the next bit is in error is greater than 1 1000.
In a thin film manufacturing process, the proportion of parts that are not acceptable is 2%.
However, the process is sensitive to contamination problems that can increase the rate of parts
that are not acceptable. If we knew that during a particular shift there were problems with the
filters used to control contamination, we would assess the probability of a part being unac-
ceptable as higher than 2%.
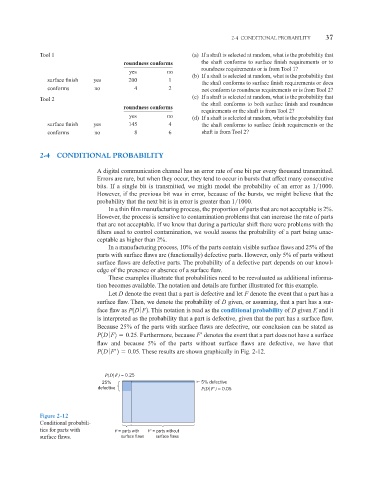
In a manufacturing process, 10% of the parts contain visible surface flaws and 25% of the
parts with surface flaws are (functionally) defective parts. However, only 5% of parts without
surface flaws are defective parts. The probability of a defective part depends on our knowl-
edge of the presence or absence of a surface flaw.
These examples illustrate that probabilities need to be reevaluated as additional informa-
tion becomes available. The notation and details are further illustrated for this example.
Let D denote the event that a part is defective and let F denote the event that a part has a
surface flaw. Then, we denote the probability of D given, or assuming, that a part has a sur-
face flaw as P1D ƒ F2 . This notation is read as the conditional probability of D given F, and it
is interpreted as the probability that a part is defective, given that the part has a surface flaw.
Because 25% of the parts with surface flaws are defective, our conclusion can be stated as
P1D ƒ F2 0.25 . Furthermore, because F¿ denotes the event that a part does not have a surface
flaw and because 5% of the parts without surface flaws are defective, we have that
P1D ƒ F¿2 0.05 . These results are shown graphically in Fig. 2-12.

P(DF) = 0.25
25% 5% defective
defective P(DF’) = 0.05

Figure 2-12
Conditional probabili-
ties for parts with F = parts with F’ = parts without
surface flaws. surface flaws surface flaws