Page 89 - Applied Statistics And Probability For Engineers

PQ220 6234F.Ch 03 13/04/2002 03:19 PM Page 67

3-4 MEAN AND VARIANCE OF A DISCRETE RANDOM VARIABLE 67

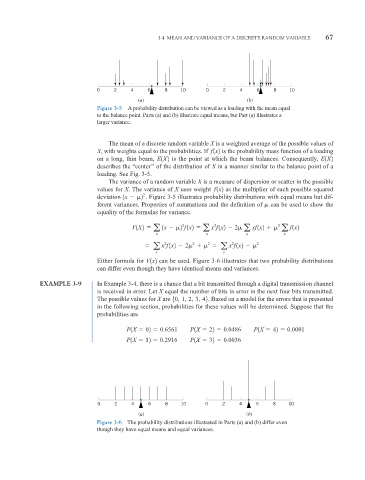
0 2 4 6 8 10 0 2 4 6 8 10
(a) (b)
Figure 3-5 A probability distribution can be viewed as a loading with the mean equal
to the balance point. Parts (a) and (b) illustrate equal means, but Part (a) illustrates a
larger variance.

The mean of a discrete random variable X is a weighted average of the possible values of
X, with weights equal to the probabilities. If f 1x2 is the probability mass function of a loading
on a long, thin beam, E1X2 is the point at which the beam balances. Consequently, E1X2
describes the “center’’ of the distribution of X in a manner similar to the balance point of a
loading. See Fig. 3-5.
The variance of a random variable X is a measure of dispersion or scatter in the possible
values for X. The variance of X uses weight f 1x2 as the multiplier of each possible squared
deviation 1x 2 2 . Figure 3-5 illustrates probability distributions with equal means but dif-
ferent variances. Properties of summations and the definition of can be used to show the
equality of the formulas for variance.

2
2
V1X2 a 1x 2 f 1x2 a x f 1x2 2 a xf 1x2 2 a f 1x2
x x x x
2
2
2
2
a x f 1x2 2 a x f 1x2 2
x x
Either formula for V1x2 can be used. Figure 3-6 illustrates that two probability distributions
can differ even though they have identical means and variances.
EXAMPLE 3-9 In Example 3-4, there is a chance that a bit transmitted through a digital transmission channel
is received in error. Let X equal the number of bits in error in the next four bits transmitted.
The possible values for X are 50, 1, 2, 3, 46 . Based on a model for the errors that is presented
in the following section, probabilities for these values will be determined. Suppose that the
probabilities are

P1X 02 0.6561 P1X 22 0.0486 P1X 42 0.0001
P1X 12 0.2916 P1X 32 0.0036

0 2 4 6 8 10 0 2 4 6 8 10
(a) (b)
Figure 3-6 The probability distributions illustrated in Parts (a) and (b) differ even
though they have equal means and equal variances.