Page 323 - Applied statistics and probability for engineers

Section 8-7/Tolerance and Prediction Intervals 301

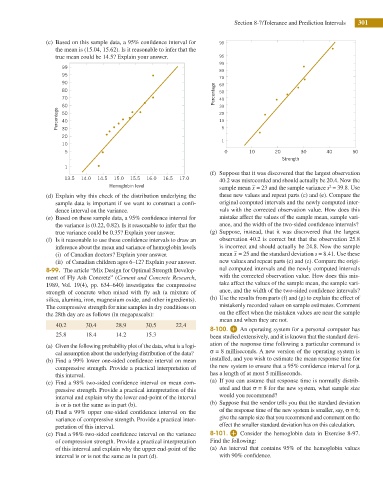
(c) Based on this sample data, a 95% conidence interval for 99
the mean is (15.04, 15.62). Is it reasonable to infer that the
true mean could be 14.5? Explain your answer. 95
90
99 80
95
70
90 60
80 Percentage 50
70 40
60 30
Percentage 50 20 5
10
40
30
20
1
10
5 0 10 20 30 40 50
Strength
1
(f) Suppose that it was discovered that the largest observation
13.5 14.0 14.5 15.0 15.5 16.0 16.5 17.0
40.2 was misrecorded and should actually be 20.4. Now the
Hemoglobin level 2
sample mean x = 23 and the sample variance s = 39.8. Use
(d) Explain why this check of the distribution underlying the these new values and repeat parts (c) and (e). Compare the
sample data is important if we want to construct a coni- original computed intervals and the newly computed inter-
dence interval on the variance. vals with the corrected observation value. How does this
(e) Based on these sample data, a 95% conidence interval for mistake affect the values of the sample mean, sample vari-
the variance is (0.22, 0.82). Is it reasonable to infer that the ance, and the width of the two-sided conidence intervals?
true variance could be 0.35? Explain your answer. (g) Suppose, instead, that it was discovered that the largest
(f) Is it reasonable to use these conidence intervals to draw an observation 40.2 is correct but that the observation 25.8
inference about the mean and variance of hemoglobin levels is incorrect and should actually be 24.8. Now the sample
(i) of Canadian doctors? Explain your answer. mean x = 25 and the standard deviation s = 8.41. Use these
(ii) of Canadian children ages 6–12? Explain your answer. new values and repeat parts (c) and (e). Compare the origi-
8-99. The article “Mix Design for Optimal Strength Develop- nal computed intervals and the newly computed intervals
ment of Fly Ash Concrete” (Cement and Concrete Research, with the corrected observation value. How does this mis-
1989, Vol. 19(4), pp. 634–640) investigates the compressive take affect the values of the sample mean, the sample vari-
strength of concrete when mixed with ly ash (a mixture of ance, and the width of the two-sided conidence intervals?
silica, alumina, iron, magnesium oxide, and other ingredients). (h) Use the results from parts (f) and (g) to explain the effect of
The compressive strength for nine samples in dry conditions on mistakenly recorded values on sample estimates. Comment
the 28th day are as follows (in megapascals): on the effect when the mistaken values are near the sample
mean and when they are not.
40.2 30.4 28.9 30.5 22.4
8-100. An operating system for a personal computer has
25.8 18.4 14.2 15.3 been studied extensively, and it is known that the standard devi-
(a) Given the following probability plot of the data, what is a logi- ation of the response time following a particular command is
cal assumption about the underlying distribution of the data? σ = 8 milliseconds. A new version of the operating system is
(b) Find a 99% lower one-sided conidence interval on mean installed, and you wish to estimate the mean response time for
compressive strength. Provide a practical interpretation of the new system to ensure that a 95% conidence interval for μ
this interval. has a length of at most 5 milliseconds.
(c) Find a 98% two-sided conidence interval on mean com- (a) If you can assume that response time is normally distrib-
pressive strength. Provide a practical interpretation of this uted and that σ = 8 for the new system, what sample size
interval and explain why the lower end-point of the interval would you recommend?
is or is not the same as in part (b). (b) Suppose that the vendor tells you that the standard deviation
(d) Find a 99% upper one-sided conidence interval on the of the response time of the new system is smaller, say, σ = 6;
variance of compressive strength. Provide a practical inter- give the sample size that you recommend and comment on the
pretation of this interval. effect the smaller standard deviation has on this calculation.
(e) Find a 98% two-sided conidence interval on the variance 8-101. Consider the hemoglobin data in Exercise 8-97.
of compression strength. Provide a practical interpretation Find the following:
of this interval and explain why the upper end-point of the (a) An interval that contains 95% of the hemoglobin values
interval is or is not the same as in part (d). with 90% conidence.