Page 186 - Artificial Intelligence for Computational Modeling of the Heart

158 Chapter 4 Data-driven reduction of cardiac models

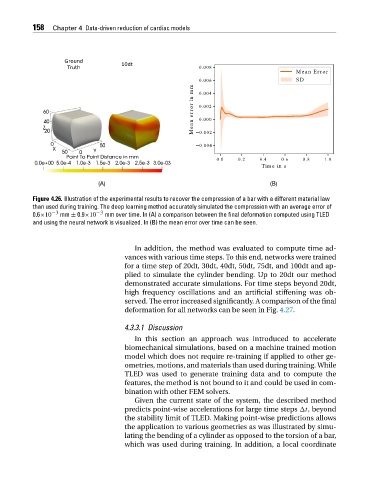
Figure 4.26. Illustration of the experimental results to recover the compression of a bar with a different material law
than used during training. The deep learning method accurately simulated the compression with an average error of
0.6×10 −3 mm ± 0.9×10 −3 mm over time. In (A) a comparison between the final deformation computed using TLED
and using the neural network is visualized. In (B) the mean error over time can be seen.

In addition, the method was evaluated to compute time ad-
vances with various time steps. To this end, networks were trained
for a time step of 20dt, 30dt, 40dt, 50dt, 75dt, and 100dt and ap-
plied to simulate the cylinder bending. Up to 20dt our method
demonstrated accurate simulations. For time steps beyond 20dt,
high frequency oscillations and an artificial stiffening was ob-
served. The error increased significantly. A comparison of the final
deformation for all networks can be seen in Fig. 4.27.

4.3.3.1 Discussion
In this section an approach was introduced to accelerate
biomechanical simulations, based on a machine trained motion
model which does not require re-training if applied to other ge-
ometries, motions, and materials than used during training. While
TLED was used to generate training data and to compute the
features, the method is not bound to it and could be used in com-
bination with other FEM solvers.
Given the current state of the system, the described method
predicts point-wise accelerations for large time steps t,beyond
the stability limit of TLED. Making point-wise predictions allows
the application to various geometries as was illustrated by simu-
lating the bending of a cylinder as opposed to the torsion of a bar,
which was used during training. In addition, a local coordinate