Page 195 - Artificial Intelligence for Computational Modeling of the Heart

Chapter 5 Machine learning methods for robust parameter estimation 167

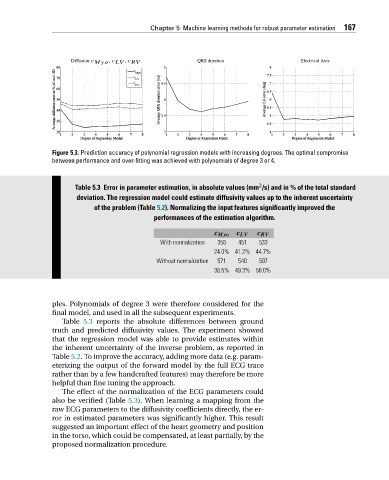
Figure 5.3. Prediction accuracy of polynomial regression models with increasing degrees. The optimal compromise
between performance and over-fitting was achieved with polynomials of degree 3 or 4.

2
Table 5.3 Error in parameter estimation, in absolute values (mm /s) and in % of the total standard
deviation. The regression model could estimate diffusivity values up to the inherent uncertainty
of the problem (Table 5.2). Normalizing the input features significantly improved the
performances of the estimation algorithm.

c Myo c LV c RV
With normalization 356 451 533
24.0% 41.2% 44.7%
Without normalization 571 540 597
38.5% 49.3% 50.0%

ples. Polynomials of degree 3 were therefore considered for the
final model, and used in all the subsequent experiments.
Table 5.3 reports the absolute differences between ground
truth and predicted diffusivity values. The experiment showed
that the regression model was able to provide estimates within
the inherent uncertainty of the inverse problem, as reported in
Table 5.2. To improve the accuracy, adding more data (e.g. param-
eterizing the output of the forward model by the full ECG trace
rather than by a few handcrafted features) may therefore be more
helpful than fine tuning the approach.
The effect of the normalization of the ECG parameters could
also be verified (Table 5.3). When learning a mapping from the
raw ECG parameters to the diffusivity coefficients directly, the er-
ror in estimated parameters was significantly higher. This result
suggested an important effect of the heart geometry and position
in the torso, which could be compensated, at least partially, by the
proposed normalization procedure.