Page 165 - Artificial Intelligence for the Internet of Everything

The Value of Information and the Internet of Things 151

We assign a random variable C to be the cost of performing on the con-
tract. Unfortunately, this cost is a probabilistic guess. We let the random var-
iable L be the random variable representing the lowest bid of the
competitors. The company’s bid is given by the random variable B. The
company’s profit is the random variable V.
If b > l, the company loses the contract, and it is profit is 0. If b < l the
company wins the contract and performs the work at a cost of c. Therefore
the profit is v ¼ b c. Hence, similarly to Eq. (9.3)(Howard, 1966), the
company gets the contract in case of a tie (b ¼ l). In terms of the random
variables:

B C, if B L
(9.1)
0, if B > L
V¼
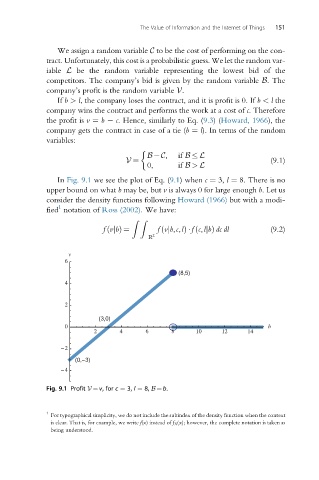
In Fig. 9.1 we see the plot of Eq. (9.1) when c ¼ 3, l ¼ 8. There is no
upper bound on what b may be, but v is always 0 for large enough b. Let us
consider the density functions following Howard (1966) but with a modi-
1
fied notation of Ross (2002). We have:
ZZ
f ðvjb,c,lÞ f ðc,ljbÞ dc dl (9.2)
f ðvjbÞ¼
 2

Fig. 9.1 Profit V¼ v, for c ¼ 3, l ¼ 8, B¼ b.

1
For typographical simplicity, we do not include the subindex of the density function when the context
is clear. That is, for example, we write f(x) instead of f X (x); however, the complete notation is taken as
being understood.