Page 191 - Autonomous Mobile Robots

Landmarks and Triangulation in Navigation 175

(a) 8
7

6
5
y (m) 4

3
2

1
0
– 4 – 3 – 2 – 1 0 1 2 3 4
x (m)

(b)
Votes

6000
5000
4000
3000
2000
1000 8
7
0 5 6
– 4 – 3 – 2 4
– 1 0 1 2 3 y (m)
x (m) 2 3 4 0 1

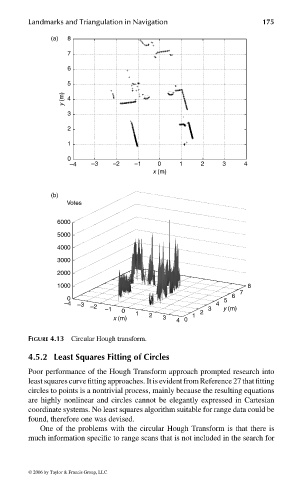
FIGURE 4.13 Circular Hough transform.

4.5.2 Least Squares Fitting of Circles

Poor performance of the Hough Transform approach prompted research into
least squares curve fitting approaches. It is evident from Reference 27 that fitting
circles to points is a nontrivial process, mainly because the resulting equations
are highly nonlinear and circles cannot be elegantly expressed in Cartesian
coordinate systems. No least squares algorithm suitable for range data could be
found, therefore one was devised.
One of the problems with the circular Hough Transform is that there is
much information specific to range scans that is not included in the search for

© 2006 by Taylor & Francis Group, LLC

FRANKL: “dk6033_c004” — 2006/3/31 — 16:42 — page 175 — #27