Page 106 - Basics of Fluid Mechanics and Introduction to Computational Fluid Dynamics

Dynamics of Inviscid Fluids 91

velocity 1m/s. The centers of the cylinders are separated by a distance

of d = 2.5m, in a direction perpendicular on the flow. Considering
panels on each cylinder, let us calculate for every 27 control points the
values of the velocity and the pressure coefficient.
We choose the simplified variant, with the boundary points on the
surface of the cylinders and the control points are the midpoints of the
panels. The variables P of the program will contain all the characteristics

of every panel.
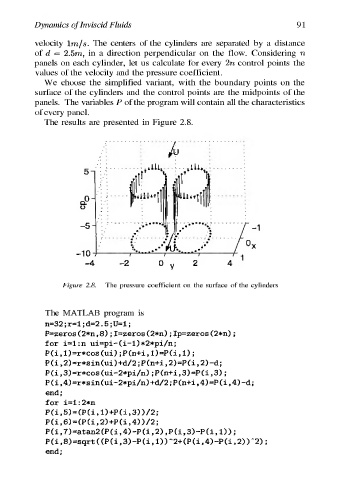
The results are presented in Figure 2.8.

Figure 2.8. The pressure coefficient on the surface of the cylinders

The MATLAB program is

n=32;r=1;d=2.5;U=1;
;
P=zeros (24#n,8) ; I=zeros(2«n) ;
Ip=zeros
(2*n)
for i=i:n ui=pi-(i-1)*2*pi/n;
P(i,1)=r*cos
;P(nti,1)=P(i,1);
(ui)
P(i,2)=r*sin(ui)+d/2;P(nti,2)=P(i,2)-d;
P(i,3)=r*cos (ui-2*pi/n) ;P(mti,3)=P(i,3);
P(i,4)=r*sin(ui-2*pi/n)+d/2;P(nti,4)=P(i,4)-d;
end;
for i=1:2*n
P(i,5)=(P(i,1)+P(i,3))/2;
P(i,6)=(P(i,2)+P(i,4))/2;

P(i,7)=atan2(P(i,4)-P(i,2),P(i,3)-P(i,1));
P(i,8)=sqrt ((P(i,3)-P(i,1))°2+(P(i,4)-P(i,2))°2);
end;