Page 37 - Battery Reference Book

1/22 Introduction to battery technology
is the partial molar entropy defined in the same way as
the partial molar energy or volume, etc. We can now
find the change of F with temperature and pressure.
First, differentiating F with respect to T, we have

and differentiating again with respect to n1,
dS -

P
since

Introducing the value of given by Equation 1.60 we
have
-
dc - F1-E1
- =s* = -
dT T
- / dividing through by T, we find
0.1
I d E c 5
- x _- - =--
T dT T2 T2
or
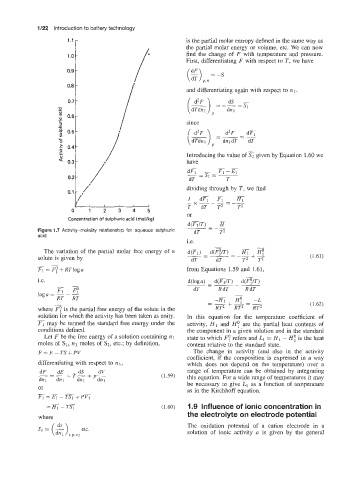
Concentration of sulphuric acid (rnol/kg)
d(6IT) = 7f
-
Figure 1.7 Activity-molality relationship for aqueous sulphuric dT --
T2
acid
i.e.
-
The variation of the partial molar free energy of a d(F1) d($/T) - % HY
T2 'F
solute is given by ~- - ~ dT - -- (1.61)
dT
- -
F1 =Fy+RTloga from Equations 1.59 and 1.61,
i.e. d(1og a) d(5IT) d(q/T)
- - -=--- R dT R dT
dT
Fi
FY
loga = - - - -
RT RT
(1.62)
is
where 3 the partial free energy of the solute in the
solution for which the activity has been taken as unity. In this equation for the temperature coefficient of
-
F1 may be termed the standard free energy under the activity, HI and H; are the partial heat contents of
conditions defined. the component in a given solution and in the standard
Let F be the free energy of a solution containing nl state to which FY refers and Li = H1 - HY is the heat
moles of SI, n2 moles of SI, etc.; by definition, content relative to the standard state.
F = E - TSt PV The change in activity (and also in the activity
coefficient, if the composition is expressed in a way
differentiating with respect to IZ 1, which does not depend on the temperature) over a
dF dE dS dV range of temperature can be obtained by integrating
- -T-++- (1.59) this equation. For a wide range of temperatures it may
dnl dnl dnl dnl
or be necessary to give L1 as a function of temperature
as in the Kirchhoff equation.
-
Fi=F-TG+P&
=?r;-Tq (1.60) I .9 Influence of ionic concentration in
where the electrolyte on electrode potential
The oxidation potential of a cation electrode in a
solution of ionic activity a is given by the general