Page 156 - Becoming Metric Wise

147
Publication and Citation Analysis

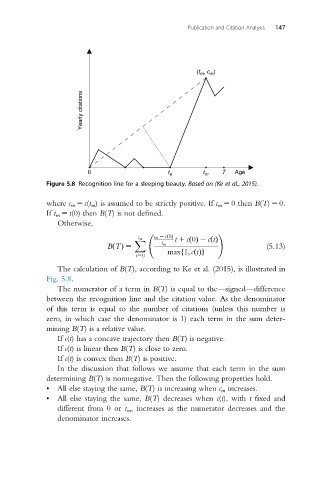
Figure 5.8 Recognition line for a sleeping beauty. Based on (Ke et al., 2015).

where c m 5 c(t m ) is assumed to be strictly positive. If c m 5 0 then B(T) 5 0.
If t m 5 t(0) then B(T) is not defined.
Otherwise,

!
c m 2 cð0Þ
t m
X t 1 cð0Þ 2 cðtÞ
BðTÞ 5 t m (5.13)
maxf1; cðtÞg
t50
The calculation of B(T), according to Ke et al. (2015), is illustrated in
Fig. 5.8.
The numerator of a term in B(T) is equal to the—signed—difference
between the recognition line and the citation value. As the denominator
of this term is equal to the number of citations (unless this number is
zero, in which case the denominator is 1) each term in the sum deter-
mining B(T) is a relative value.
If c(t) has a concave trajectory then B(T) is negative.
If c(t) is linear then B(T) is close to zero.
If c(t) is convex then B(T) is positive.
In the discussion that follows we assume that each term in the sum
determining B(T) is nonnegative. Then the following properties hold.
• All else staying the same, B(T) is increasing when c m increases.
• All else staying the same, B(T) decreases when c(t), with t fixed and
different from 0 or t m , increases as the numerator decreases and the
denominator increases.