Page 239 - Becoming Metric Wise

230 Becoming Metric-Wise

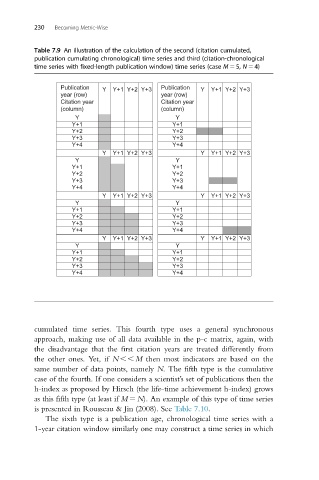
Table 7.9 An illustration of the calculation of the second (citation cumulated,
publication cumulating chronological) time series and third (citation-chronological
time series with fixed-length publication window) time series (case M 5 5, N 5 4)

Publication Y Y+1 Y+2 Y+3 Publication Y Y+1 Y+2 Y+3
year (row) year (row)
Citation year Citation year
(column) (column)
Y Y
Y+1 Y+1
Y+2 Y+2
Y+3 Y+3
Y+4 Y+4
Y Y+1 Y+2 Y+3 Y Y+1 Y+2 Y+3
Y Y
Y+1 Y+1
Y+2 Y+2
Y+3 Y+3
Y+4 Y+4
Y Y+1 Y+2 Y+3 Y Y+1 Y+2 Y+3
Y Y
Y+1 Y+1
Y+2 Y+2
Y+3 Y+3
Y+4 Y+4
Y Y+1 Y+2 Y+3 Y Y+1 Y+2 Y+3
Y Y
Y+1 Y+1
Y+2 Y+2
Y+3 Y+3
Y+4 Y+4

cumulated time series. This fourth type uses a general synchronous
approach, making use of all data available in the p-c matrix, again, with
the disadvantage that the first citation years are treated differently from
the other ones. Yet, if N ,, M then most indicators are based on the
same number of data points, namely N. The fifth type is the cumulative
case of the fourth. If one considers a scientist’s set of publications then the
h-index as proposed by Hirsch (the life-time achievement h-index) grows
as this fifth type (at least if M 5 N). An example of this type of time series
is presented in Rousseau & Jin (2008). See Table 7.10.
The sixth type is a publication age, chronological time series with a
1-year citation window similarly one may construct a time series in which