Page 90 - Becoming Metric Wise

80 Becoming Metric-Wise

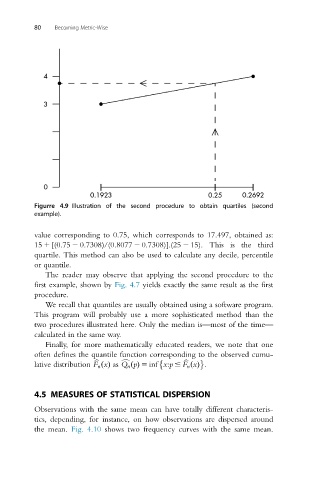
Figurre 4.9 Illustration of the second procedure to obtain quartiles (second
example).

value corresponding to 0.75, which corresponds to 17.497, obtained as:
15 1 [(0.75 2 0.7308)/(0.8077 2 0.7308)].(25 2 15). This is the third
quartile. This method can also be used to calculate any decile, percentile
or quantile.
The reader may observe that applying the second procedure to the
first example, shown by Fig. 4.7 yields exactly the same result as the first
procedure.
We recall that quantiles are usually obtained using a software program.
This program will probably use a more sophisticated method than the
two procedures illustrated here. Only the median is—most of the time—
calculated in the same way.
Finally, for more mathematically educated readers, we note that one
often defines the quantile function corresponding to the observed cumu-

lative distribution b F n ðxÞ as Q n ðpÞ 5 inf x:p # b F n ðxÞ .
c

4.5 MEASURES OF STATISTICAL DISPERSION
Observations with the same mean can have totally different characteris-
tics, depending, for instance, on how observations are dispersed around
the mean. Fig. 4.10 shows two frequency curves with the same mean.