Page 133 - Biaxial Multiaxial Fatigue and Fracture

118 G.B. MARQUIS AND I? KARJALAINEN-ROIKONEN

Based on the current experiments, Eq. (7) should be modified for nodular iron so that stress
ratio effect takes on a maximum value equal to zero regardless of the stress state. In other
words, the fatigue limit is reduced for biaxial stress ratios less than zero but is not
correspondingly increased for biaxial stress ratios greater than zero. The fatigue limit for this
material cannot exceed that observed during uniaxial tension fatigue. Equation (7) is modified
in the following way:

K=O forh>O
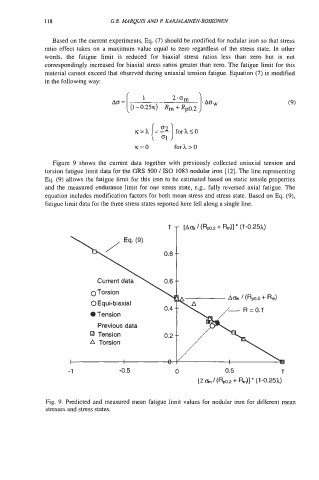
Figure 9 shows the current data together with previously collected uniaxial tension and
torsion fatigue limit data for the GRS 500 I IS0 1083 nodular iron [ 121. The line representing
Eq. (9) allows the fatigue limit for this iron to be estimated based on static tensile properties
and the measured endurance limit for one stress state, e.g., fully reversed axial fatigue. The
equation includes modification factors for both mean stress and stress state. Based on Eq. (9),
fatigue limit data for the three stress states reported here fell along a single line.

Current data \ 0.6 +

OTorsion
A% 1 (Rp0.z + Rm)
0 Equi-biaxial
0 Tension
Previous data
Tension 0.2
Torsion

Fig. 9. Predicted and measured mean fatigue limit values for nodular iron for different mean
stresses and stress states.