Page 281 - Big Data Analytics for Intelligent Healthcare Management

11.5 PROPOSED MODEL 275

Start

Initialize the population of cluster centers (solutes) “P”
Ctr = 1

Movement of solute by using Eq. (11.1)
Compute fr by using Eq. (11.2)
Ctr = Ctr+1
Evaluate fitness ‘f ’ of each solute using Eq. (11.6)
Yes
IS solute Yes No
better than
Filtered blood (FB) IS f > fr
worst solute
in “P”
Waste (W)
Update “P” by using FP
No
Movement of solute by using Eq. (11.1)
No
Is stopping
criteria is No Evalute fitness ‘f ’ of each solute using Eq. (11.6)
met
Yes Yes
Is solute is Yes
better than IS f > fr
Find best solute from “P”
worst solute
in “P”
No
Stop
Add randomness on solutes
and generate new solute

Yes Is solute
better than
worst solute
in “P” No

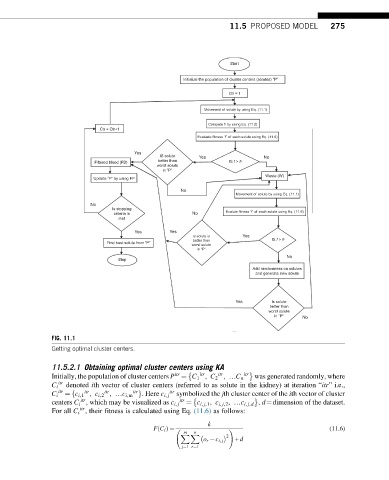
FIG. 11.1
Getting optimal cluster centers.

11.5.2.1 Obtaining optimal cluster centers using KA
itr itr itr itr
Initially, the population of cluster centers P ¼ C 1 , C 2 , …C n was generated randomly, where
itr
C i denoted ith vector of cluster centers (referred to as solute in the kidney) at iteration “itr” i.e.,
itr itr itr itr itr
f
C i ¼ c i,1 , c i,2 , …c i,m g. Here c i, j symbolized the jth cluster center of the ith vector of cluster
itr itr
centers C i , which may be visualized as c i, j ¼ c i, j,1 , c i, j,2 , …c i, j,d , d¼dimension of the dataset.
itr
For all C i , their fitness is calculated using Eq. (11.6) as follows:
k
ðÞ
FC i ¼ ! (11.6)
m n
2
XX
o r c i, j + d
j¼1 r¼1