Page 425 - Biomimetics : Biologically Inspired Technologies

Bar-Cohen : Biomimetics: Biologically Inspired Technologies DK3163_c016 Final Proof page 411 21.9.2005 11:49pm

Biomimetic and Biologically Inspired Control 411

2.5 2.5
2 Joint 1 2 Joint 2
angle [rad] 1.5 1 angle [rad] 1.5 1

0.5
0.5
0 0
Joint 2 Joint 1
−0.5 −0.5
0 0.1 0.2 0.3 0.4 0.5 0 0.1 0.2 0.3 0.4 0.5
time (s) time (s)
Optimal and semi-optimal optimal and semi-optimal
joint angles joint angles
1.6 2
1.4 Joint 1
1.2 1 1 Joint 1
velocity [rad/s] 0.8 velocity [rad/s] −1 0
0.6
0.4
0.2 Joint 2 −2 Joint 1
0
−0.2 −3
0 0.1 0.2 0.3 0.4 0.5 0 0.1 0.2 0.3 0.4 0.5
time (s) time (s)
optimal and semi-optimal optimal and semi-optimal
joint velocities joint velocities
3 3
Joint 1 2
2
1 Joint 1 Joint 2
torque [Nm] −1 0 Joint 2 torque [Nm] 0
1
−2 −1
−2
−3 −3
0 0.1 0.2 0.3 0.4 0.5 0 0.1 0.2 0.3 0.4 0.5
time (s) time (s)
optimal and semi-optimal optimal and semi-optimal
joint torques joint torques
(a) The motion from S to E1 (b) The motion from S to E2
T2 T3
0.5 E2
0.4 E1
y - position [m] 0.3 S

0.2
T1 T4
0.1 teaching information
start position
end position
optimal trajectory
0 semi-optimal trajectory
0 0.1 0.2 0.3 0.4 0.5
x - position [m]
(c) The trajectories in the task space
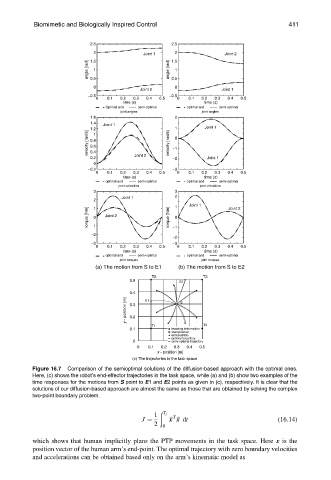
Figure 16.7 Comparison of the semioptimal solutions of the diffusion-based approach with the optimal ones.
Here, (c) shows the robot’s end-effector trajectories in the task space, while (a) and (b) show two examples of the
time responses for the motions from S point to E1 and E2 points as given in (c), respectively. It is clear that the
solutions of our diffusion-based approach are almost the same as those that are obtained by solving the complex
two-point boundary problem.
ð
1 T f ::: T :::
J ¼ x x dt (16:14)
2 0

which shows that human implicitly plans the PTP movements in the task space. Here x is the
position vector of the human arm’s end-point. The optimal trajectory with zero boundary velocities
and accelerations can be obtained based only on the arm’s kinematic model as