Page 343 - Cam Design Handbook

THB11 9/19/03 7:33 PM Page 331

CAM SYSTEM MODELING 331

2
l Ê ˆ
1
M = mÁ ˜ . (11.39)
eq
l Ë ¯
2
The mass associated with the equivalent model therefore depends upon the amount of
mechanical advantage provided by the lever formed by the rod and the pivot.
There are two ways to calculate the equivalent mass of a system. The first is to balance
reaction forces as in the example above. This method has an advantage in that the equa-
tions of motion are developed concurrently, though it is the more tedious of the two
approaches. The other method is to consider the kinetic energy of the original model and
the lumped model. Masses and inertias store energy in the form of kinetic energy, so for
the lumped model to represent the original, the kinetic energy of the two systems must be
the same. This works not only for masses but also for inertias, as demonstrated in the fol-
lowing example.
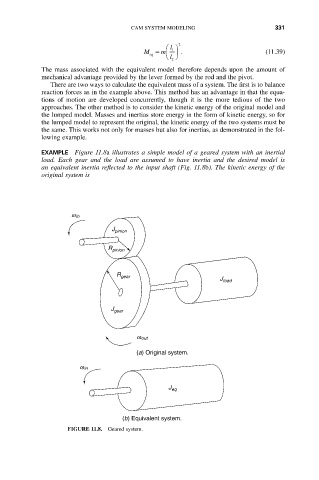
EXAMPLE Figure 11.8a illustrates a simple model of a geared system with an inertial
load. Each gear and the load are assumed to have inertia and the desired model is
an equivalent inertia reflected to the input shaft (Fig. 11.8b). The kinetic energy of the
original system is

w in
J pinion

R pinion

R gear
J load

J gear

w out
(a) Original system.

w in

J eq

(b) Equivalent system.
FIGURE 11.8. Geared system.