Page 90 - Carbon Nanotubes

Helically coiled and toroidal cage forms of graphitic carbon 19

pentagons- heptagons ergies of the tori[12,20,21]. To confirm the thermo-
dynamic stability, simulations at higher temperatures
using a second-order equations-of-motion method
were also performed. For details see ref. [13].
For the tori c360, C240, c540, and C576, the values
of the cohesive energies per atom are -7.41, -7.33,
-7.40, and -7.39 eV, respectively. Because the torus
C240 has the highest ratio of the number of pentagons
and heptagons to hexagons among them, torus C240
affects the distortion caused by the insertion of pent-
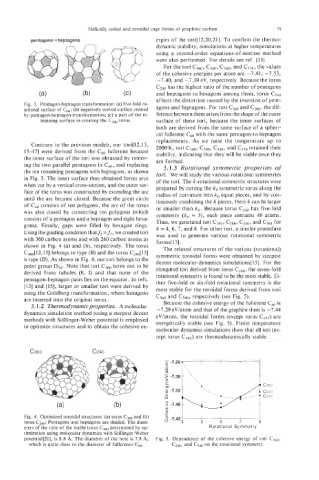
Fig. 3. Pentagon-heptagon transformation: (a) five-fold ro-
tational surface of c,; (b) negatively curved surface created agons and heptagons. For tori C240 and c360, the dif-
by pentagon-heptagon transformation; (c) a part of the re- ference between them arises from the shape of the outer
maining surface in creating the C3, torus. surface of these tori, because the inner surfaces of
both are derived from the same surface of a spheri-
cal fullerene Ca with the same pentagon-to-heptagon
replacements. As we raise the temperature up to
Contrary to the previous models, our tori[12,13,
15-17] were derived from the c60 fullerene because 2000K, tori C360, C240, c540, and c576 retained their
stability, indicating that they will be viable once they
the inner surface of the tori was obtained by remov-
ing the two parallel pentagons in c60, and replacing are formed.
3.1.3 Rotational symmetric properties of
the ten remaining pentagons with heptagons, as shown tori. We will study the various rotational symmetries
in Fig. 3. The inner surface thus obtained forms arcs
when cut by a vertical cross-section, and the outer sur- of the tori. The k-rotational symmetric structures were
prepared by cutting the ko symmetric torus along the
face of the torus was constructed by extending the arc radius of curvature into ko equal pieces, and by con-
until the arc became closed. Because the great circle tinuously combining the k pieces. Here k can be larger
of c60 consists of ten polygons, the arc of the torus or smaller than ko. Because torus C240 has five-fold
was also closed by connecting ten polygons (which symmetry (ko = 9, each piece contains 48 atoms.
consists of a pentagon and a heptagon and eight hexa-
gons). Finally, gaps were filled by hexagon rings. Thus, we generated tori C192, CZs8, c336, and C384 for
k = 4,6,7, and 8. For other tori, a similar procedure
Using the guiding condition thatf, = f7, we created tori was used to generate various rotational symmetric
with 360 carbon atoms and with 240 carbon atoms as forms[l5].
shown in Fig. 4 (a) and (b), respectively. The torus
C360[ 12,131 belongs to type (B) and the torus C240[ 151 The relaxed structures of the various (rotational)
is type (D). As shown in Fig. 4, our tori belongs to the symmetric toroidal forms were obtained by steepest
point group D5d. Note that tori c360 turns out to be decent molecular-dynamics simulations[ 151. For the
derived from tubules (8, 2) and that none of the elongated tori derived from torus C240, the seven-fold
rotational symmetry is found to be the most stable. Ei-
pentagon-heptagon pairs lies on the equator. In refs. ther five-fold or six-fold rotational symmetry is the
[13] and [15], larger or smaller tori were derived by most stable for the toroidal forms derived from tori
using the Goldberg transformation, where hexagons
are inserted into the original torus. c360 and 0, respectively (see Fig. 5).
Because the cohesive energy of the fullerene c60 is
3.1.2 Thermodynamic properties. A molecular- -7.29 eV/atom and that of the graphite sheet is -7.44
dynamics simulation method (using a steepest decent eV/atom, the toroidal forms (except torus C192) are
method) with Stillinger-Weber potential is employed energetically stable (see Fig. 5). Finite temperature
to optimize structures and to obtain the cohesive en-
molecular-dynamics simulations show that all tori (ex-
cept torus CL9J are thermodynamically stable.

c360 c240

c360
c540
c240

2L
Fig. 4. Optimized toroidal structures: (a) torus C3, and (b) 8 4 5 6 7 a
-7.45
torus CZm; Pentagons and heptagons are shaded. The diam-
eters of the tube of the stable torus C360 determined by op- Rotational Sy m m et ry
timization using molqcular dynamics with Stillinger-Weber
potential[21], is 8.8 A. The diameter of the hole is 7.8 A, Fig. 5. Dependence of the cohesive energy of tori C360,
which is quite close to the diameter of fullerence CG0. C,,,, and C,,, on the rotational symmetry.