Page 28 - Chalcogenide Glasses for Infrared Optics

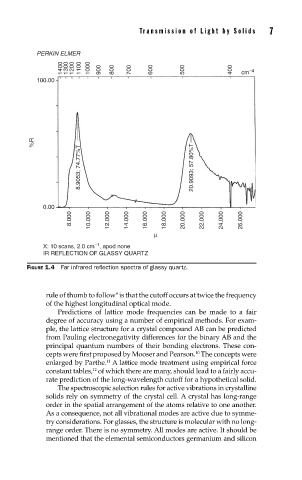
Transmission of Light by Solids 7

PERKIN ELMER
1400 1300 1200 1100 1000 900 800 700 600 500 400 cm –4

100.00

%R
8.9053; 74.77%T 20.9093; 57.80%T

0.00
8.000 10.000 12.000 14.000 16.000 18.000 20.000 22.000 24.000 26.000

µ
–1
X: 10 scans, 2.0 cm , apod none
IR REFLECTION OF GLASSY QUARTZ
FIGURE 1.4 Far infrared refl ection spectra of glassy quartz.

9
rule of thumb to follow is that the cutoff occurs at twice the frequency
of the highest longitudinal optical mode.
Predictions of lattice mode frequencies can be made to a fair
degree of accuracy using a number of empirical methods. For exam-
ple, the lattice structure for a crystal compound AB can be predicted
from Pauling electronegativity differences for the binary AB and the
principal quantum numbers of their bonding electrons. These con-
10
cepts were first proposed by Mooser and Pearson. The concepts were
enlarged by Parthe. A lattice mode treatment using empirical force
11
12
constant tables, of which there are many, should lead to a fairly accu-
rate prediction of the long-wavelength cutoff for a hypothetical solid.
The spectroscopic selection rules for active vibrations in crystalline
solids rely on symmetry of the crystal cell. A crystal has long-range
order in the spatial arrangement of the atoms relative to one another.
As a consequence, not all vibrational modes are active due to symme-
try considerations. For glasses, the structure is molecular with no long-
range order. There is no symmetry. All modes are active. It should be
mentioned that the elemental semiconductors germanium and silicon