Page 348 - Chemical Process Equipment - Selection and Design

11.2. THEORY OF FILTRATION 311

EXAMPLE XL.2 trapezoidal rule:
Filtration Process with a Centrifu al Charge Pump
4
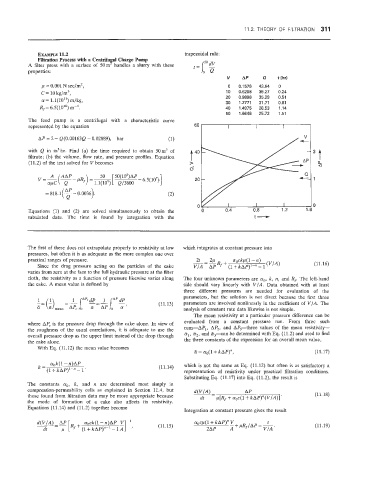
A filter press with a surface of 50m handles a slurry with these
properties:
V AP 0 t(hs)
y = 0.001 N seclm', 0 0.1576 43.64 0
C = 10 kg,'m3, 10 0.6208 39.27 0.24
1.1(1O") Q'Il/kg, 20 0.9896 35.29 0.51
0.81
1.2771 31.71
30
Rf = 6.5(101') m-'. 40 1.4975 28.53 7.14
50 1.6648 25.72 1.51
The feed pump is a centrifugal with a characteristic curve
represented by the equation
AP = 2 - Q(0.00163Q - 0.02889), bar (1)
with Q in m38.ir. Find (a) the time required to obtain 50m3 of
filtrate; (b) the volume, flow rate, and pressure profiles. Equation t 40
(11.2) of the text solved for V becomes > P a
d
d
20 1

(: )
=818.1 --0.0036 .
a 0
Equations (1) and (2) are solved simultaneously to obtain the 0 0.4 0.8 4.2
tabulated data. The time is found by integration with the t-

The first of these does not extrapolate properly to resistivity at low which integrates at constant pressure into
pressures, but often it is as adequate as the more complex one over
2t
practical ranges of pressure. __=_ 2y a,ckp(l - n) (11.16)
Since the drag pressure acting on the particles of the cake VIA AP Rf + (1 + /CAP)'-" - 1 (VIA)
varies from zero at the face to the full hydraulic pressure at the filter
cloth, the resistivity a5 a function of pressure likewise varies along The four unknown parameters are a', k, n, and RP The left-hand
the cake. A mean value is defined by side should vary linearly with VIA. Data obtained with at least
three different pressures are needed for evaluation of the
parameters, but the solution is not direct because the first three
(11.13) parameters are involved nonlinearly in the coefficient of VIA. The
analysis of constant rate data likewise is not simple.
The mean resistivity at a particular pressure difference can be
where AP, is the pressure drop through the cake alone. In view of evaluated from a constant pressure run. From three such
the roughness of the usual correlations, it is adequate to use the runs-AP,, AP2, and AP,--three values of the mean resistivity-
overall pressure drop as the upper limit instead of the drop through &,, &2, and E3-can be determined with Eq. (11.2) and used to find
the cake done. the three constants of the expression for an overall mean value,
With Eq. (l1.12) the mean value becomes
& = ao(l + /CAP)", (11.17)
a0k(3. - n)AP
&= (11.14) which is not the same as Eq. (11.12) but often is as satisfactory a
(1 3 kbdy" - 1 representation of resistivity under practical filtration conditions.
Substituting Eq. (11.17) into Eq. (11.2), the result is
The constants a', k, and n are determined most simply in
compression-permeability cells as explained in Section 11.4, but
those found from filtration data may be more appropriate because (11.18)
the mode of formation of a cake also affects its resistivity.
Equations (11.2.4) and (11.2) together become Integration at constant pressure gives the result

(11.19)