Page 287 - Chiral Separation Techniques

266 10 The Use of SMB for the Manufacture of Enantiopure Drug Substances: From …

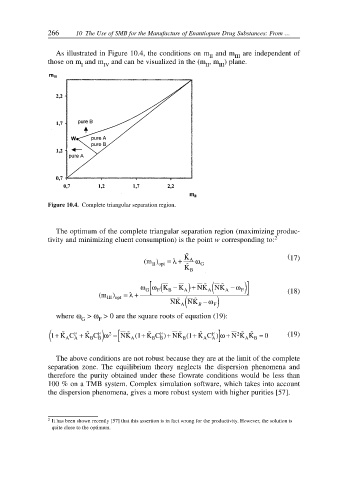
As illustrated in Figure 10.4, the conditions on m and m are independent of
II III
those on m and m and can be visualized in the (m ,m ) plane.
I IV II III

Figure 10.4. Complete triangular separation region.

The optimum of the complete triangular separation region (maximizing produc-
tivity and minimizing eluent consumption) is the point w corresponding to: 2

˜
(m ) = λ + K A ω ( 17)
II opt ˜ G
K B
G[
ωω F( K − K A) + NK A( NK − ω F)]
˜
˜
A
B
(m ) = λ + A( F) (18)
III opt
˜
˜
NK NK − ω
B
where ω > ω > 0 are the square roots of equation (19):
G F
]
( 1+ K C F A + KC ω 2 − NK (1 KC ) NK (1 K C ) ω + N K K B = 0 (19)
) [
˜ ˜
+
+
˜
˜
˜
˜
˜
+
˜
F
F
F
2
A
A
A
BB
B
A
A
B B
The above conditions are not robust because they are at the limit of the complete
separation zone. The equilibrium theory neglects the dispersion phenomena and
therefore the purity obtained under these flowrate conditions would be less than
100 % on a TMB system. Complex simulation software, which takes into account
the dispersion phenomena, gives a more robust system with higher purities [57].
2 It has been shown recently [57] that this assertion is in fact wrong for the productivity. However, the solution is
quite close to the optimum.