Page 189 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

178 SUPERVISED LEARNING

(a) (b)
1 10 0
1 error
measure of eccentricity 0.6 0.5 mse 10 –1
0.8

0.4
–2
10
0.2
0
0 10 –3
0 0.2 0.4 0.6 0.8 1 0 100 200 300 400 500
measure of six-fold rotational symmetry epoch

(c) (d)
0.8 10 0
1
0.7 error
measure of eccentricity 0.6 0.5 mse 10 –1
0.8
0.6
0.4
0.4
0.3
–2
10
0.2
0 0.2
0.1
0 0.2 0.4 0.6 0.8 1 0 10 –3
0 200 400 600 800 1000
measure of six-fold rotational symmetry
epoch
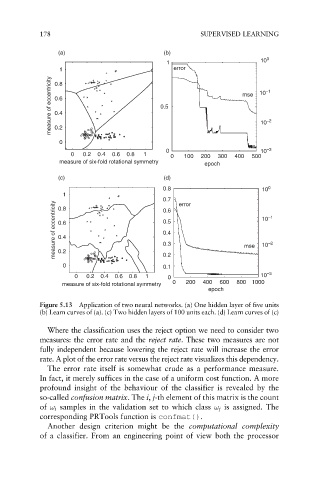
Figure 5.13 Application of two neural networks. (a) One hidden layer of five units
(b) Learn curves of (a). (c) Two hidden layers of 100 units each. (d) Learn curves of (c)

Where the classification uses the reject option we need to consider two
measures: the error rate and the reject rate. These two measures are not
fully independent because lowering the reject rate will increase the error
rate. A plot of the error rate versus the reject rate visualizes this dependency.
The error rate itself is somewhat crude as a performance measure.
In fact, it merely suffices in the case of a uniform cost function. A more
profound insight of the behaviour of the classifier is revealed by the
so-called confusion matrix. The i, j-th element of this matrix is the count
of ! i samples in the validation set to which class ! j is assigned. The
corresponding PRTools function is confmat().
Another design criterion might be the computational complexity
of a classifier. From an engineering point of view both the processor