Page 191 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

180 SUPERVISED LEARNING

^
Usually, the required number of samples N Test is defined such that E is
E
within some specified margin around the true E with a prescribed prob-
ability. It can be calculated from the posterior probability density
p(Ejn error , N Test ). See exercise 5. However, we take our ease by simply
=E is equal to some fixed
E
requiring that the relative uncertainty ^ E
fraction
. Substitution in (5.68) and solving for N Test we obtain:
1 E
N Test ¼ ð5:69Þ
2

E
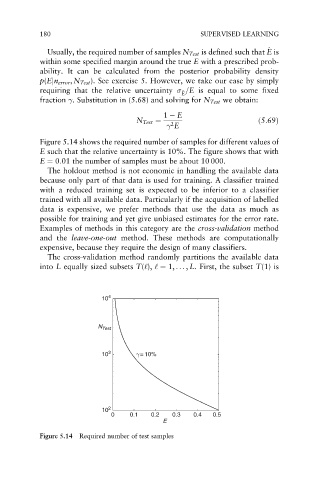
Figure 5.14 shows the required number of samples for different values of
E such that the relative uncertainty is 10%. The figure shows that with
E ¼ 0:01 the number of samples must be about 10 000.
The holdout method is not economic in handling the available data
because only part of that data is used for training. A classifier trained
with a reduced training set is expected to be inferior to a classifier
trained with all available data. Particularly if the acquisition of labelled
data is expensive, we prefer methods that use the data as much as
possible for training and yet give unbiased estimates for the error rate.
Examples of methods in this category are the cross-validation method
and the leave-one-out method. These methods are computationally
expensive, because they require the design of many classifiers.
The cross-validation method randomly partitions the available data
into L equally sized subsets T(‘), ‘ ¼ 1, .. . , L. First, the subset T(1) is

10 4

N Test

10 3 γ = 10%

10 2
0 0.1 0.2 0.3 0.4 0.5
E
Figure 5.14 Required number of test samples