Page 195 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

184 FEATURE EXTRACTION AND SELECTION

0.5

0.45 E
0.4

0.35
0.3 N =20
error rate 0.25
S

0.2 N =80
S
0.15
0.1

0.05
E min (N = ∞)
S
0
2 4 6 8 10 12
N
dimension of measurement space
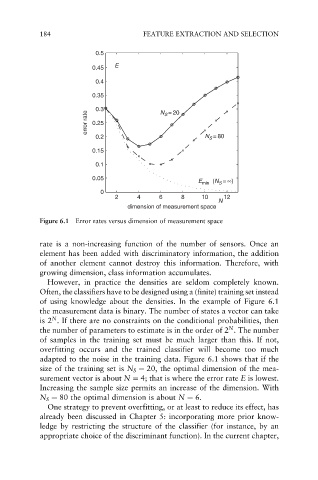
Figure 6.1 Error rates versus dimension of measurement space

rate is a non-increasing function of the number of sensors. Once an
element has been added with discriminatory information, the addition
of another element cannot destroy this information. Therefore, with
growing dimension, class information accumulates.
However, in practice the densities are seldom completely known.
Often, the classifiers have to be designed using a (finite) training set instead
of using knowledge about the densities. In the example of Figure 6.1
the measurement data is binary. The number of states a vector can take
N
is 2 . If there are no constraints on the conditional probabilities, then
N
the number of parameters to estimate is in the order of 2 . The number
of samples in the training set must be much larger than this. If not,
overfitting occurs and the trained classifier will become too much
adapted to the noise in the training data. Figure 6.1 shows that if the
size of the training set is N S ¼ 20, the optimal dimension of the mea-
surement vector is about N ¼ 4; that is where the error rate E is lowest.
Increasing the sample size permits an increase of the dimension. With
N S ¼ 80 the optimal dimension is about N ¼ 6.
One strategy to prevent overfitting, or at least to reduce its effect, has
already been discussed in Chapter 5: incorporating more prior know-
ledge by restricting the structure of the classifier (for instance, by an
appropriate choice of the discriminant function). In the current chapter,