Page 344 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

TIME-OF-FLIGHT ESTIMATION OF AN ACOUSTIC TONE BURST 333

filter responses
1 λ (n ) n =1
10
10 0 i
n =2
10 –1

–2 i
10
n =3
–3
10
i
–4
10
n =4
10 –5
0 5 10 15 20 25 30
n i
n =5

12000 γ (n )
i
10000 n =6

8000 i
n =7
6000

4000 i
n =8
2000
i
0
0 5 10 15 20 25 30
n
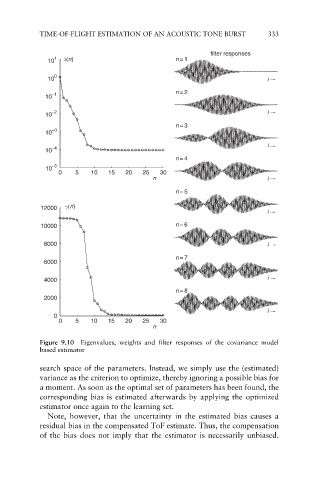
Figure 9.10 Eigenvalues, weights and filter responses of the covariance model
based estimator

search space of the parameters. Instead, we simply use the (estimated)
variance as the criterion to optimize, thereby ignoring a possible bias for
a moment. As soon as the optimal set of parameters has been found, the
corresponding bias is estimated afterwards by applying the optimized
estimator once again to the learning set.
Note, however, that the uncertainty in the estimated bias causes a
residual bias in the compensated ToF estimate. Thus, the compensation
of the bias does not imply that the estimator is necessarily unbiased.