Page 60 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB
P. 60
BAYESIAN ESTIMATION 49
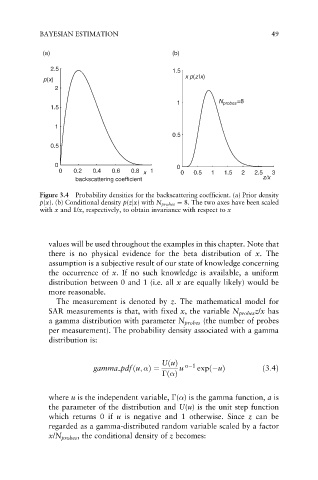
(a) (b)
2.5 1.5
x p(z|x)
p(x)
2
1 N probes =8
1.5
1
0.5
0.5
0 0
0 0.2 0.4 0.6 0.8 x 1 0 0.5 1 1.5 2 2.5 3
backscattering coefficient z/x
Figure 3.4 Probability densities for the backscattering coefficient. (a) Prior density
p(x). (b) Conditional density p(zjx) with N probes ¼ 8. The two axes have been scaled
with x and 1/x, respectively, to obtain invariance with respect to x
values will be used throughout the examples in this chapter. Note that
there is no physical evidence for the beta distribution of x. The
assumption is a subjective result of our state of knowledge concerning
the occurrence of x. If no such knowledge is available, a uniform
distribution between 0 and 1 (i.e. all x are equally likely) would be
more reasonable.
The measurement is denoted by z. The mathematical model for
SAR measurements is that, with fixed x, the variable N probes z/x has
a gamma distribution with parameter N probes (the number of probes
per measurement). The probability density associated with a gamma
distribution is:
UðuÞ 1
gamma pdfðu; Þ¼ u expð uÞ ð3:4Þ
ð Þ
where u is the independent variable, ( ) is the gamma function, a is
the parameter of the distribution and U(u) is the unit step function
which returns 0 if u is negative and 1 otherwise. Since z can be
regarded as a gamma-distributed random variable scaled by a factor
x/N probes , the conditional density of z becomes: