Page 63 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

52 PARAMETER ESTIMATION

Table 3.1 gives the solutions that are obtained if x is a scalar. The
MMSE and the MAP estimators will be worked out for the vectorial
case in the next sections. But first, the scalar case will be illustrated by
means of an example.

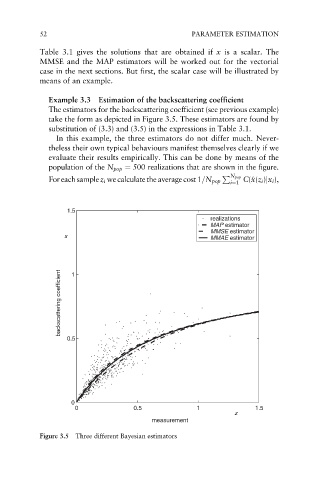
Example 3.3 Estimation of the backscattering coefficient
The estimators for the backscattering coefficient (see previous example)
take the form as depicted in Figure 3.5. These estimators are found by
substitution of (3.3) and (3.5) in the expressions in Table 3.1.
In this example, the three estimators do not differ much. Never-
theless their own typical behaviours manifest themselves clearly if we
evaluate their results empirically. This can be done by means of the
population of the N pop ¼ 500 realizations that are shown in the figure.
N pop
P
x
Foreachsample z i wecalculatetheaveragecost1=N pop i¼1 C(^ x(z i )jx i ),
1.5
realizations
MAP estimator
MMSE estimator
x MMAE estimator

backscattering coefficient 1

0.5

0
0 0.5 1 1.5
z
measurement
Figure 3.5 Three different Bayesian estimators