Page 141 - Complementarity and Variational Inequalities in Electronics

132 Complementarity and Variational Inequalities in Electronics

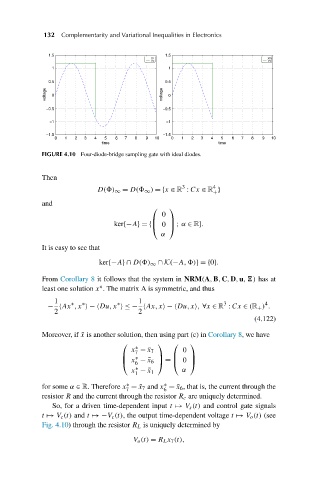
FIGURE 4.10 Four-diode-bridge sampling gate with ideal diodes.

Then
3 4
D( ) ∞ = D( ∞ ) ={x ∈ R : Cx ∈ R }
+
and
⎛ ⎞
0
ker{−A}={⎝ 0 ⎠ ; α ∈ R}.
⎜
⎟
α
It is easy to see that

ker{−A}∩ D( ) ∞ ∩ K(−A, )}={0}.

From Corollary 8 it follows that the system in NRM(A,B,C,D,u, ) has at
∗
least one solution x . The matrix A is symmetric, and thus
1 1 3 4
∗
∗
∗
− Ax ,x −ÐDu,x ≤− Ax,x −ÐDu,x , ∀x ∈ R : Cx ∈ (R + ) .
2 2
(4.122)
Moreover, if ¯x is another solution, then using part (c) in Corollary 8,wehave
⎛ ⎞ ⎛ ⎞
∗
x −¯x 7 0
7
∗
⎜ ⎟ ⎜ ⎟
6
⎝ x −¯x 6 ⎠ = ⎝ 0 ⎠
∗ α
x −¯x 1
1
∗
for some α ∈ R. Therefore x =¯x 7 and x =¯x 6 , that is, the current through the
∗
7 6
resistor R and the current through the resistor R c are uniquely determined.
So, for a driven time-dependent input t à V s (t) and control gate signals
t à V c (t) and t à − V c (t), the output time-dependent voltage t à V o (t) (see
Fig. 4.10) through the resistor R L is uniquely determined by
V o (t) = R L x 7 (t),