Page 182 - Computational Fluid Dynamics for Engineers

5.7 Convergence and Stability 169

tf

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

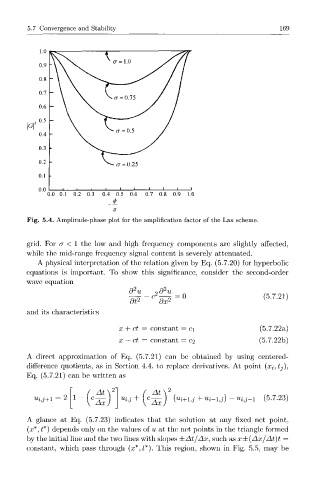
Fig. 5.4. Amplitude-phase plot for the amplification factor of the Lax scheme.

grid. For a < 1 the low and high frequency components are slightly affected,
while the mid-range frequency signal content is severely attenuated.
A physical interpretation of the relation given by Eq. (5.7.20) for hyperbolic
equations is important. To show this significance, consider the second-order
wave equation
,cPu
2 2 0 (5.7.21)
dt dx
and its characteristics

x + ct = constant = c\ (5.7.22a)
x — ct = constant = C2 (5.7.22b)
A direct approximation of Eq. (5.7.21) can be obtained by using centered-
difference quotients, as in Section 4.4. to replace derivatives. At point (xi,tj),
Eq. (5.7.21) can be written as
2
/ At\ ] ( At\ 2
Uij+1 = 2

A glance at Eq. (5.7.23) indicates that the solution at any fixed net point,
(#*, t*) depends only on the values of u at the net points in the triangle formed
by the initial line and the two lines with slopes ±AtjAx, such as x±(Ax/At)t =
constant, which pass through (#*,£*). This region, shown in Fig. 5.5, may be