Page 183 - Computational Fluid Dynamics for Engineers

170 5. Numerical Methods for Model Hyperbolic Equations

(*V*)

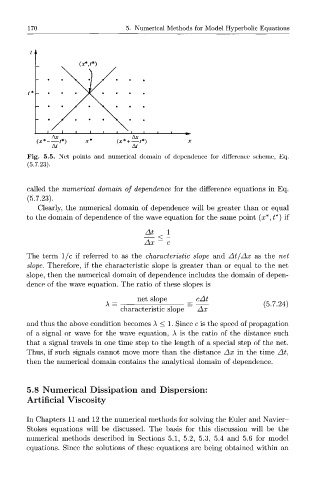
Fig. 5.5. Net points and numerical domain of dependence for difference scheme, Eq.
(5.7.23).

called the numerical domain of dependence for the difference equations in Eq.
(5.7.23).
Clearly, the numerical domain of dependence will be greater than or equal
to the domain of dependence of the wave equation for the same point (#*, t*) if

At 1
< -
Ax c
The term 1/c if referred to as the characteristic slope and At/Ax as the net
slope. Therefore, if the characteristic slope is greater than or equal to the net
slope, then the numerical domain of dependence includes the domain of depen-
dence of the wave equation. The ratio of these slopes is

n e t S l 0 p e
A = u , ^ ^ (5.7.24)
characteristic slope Ax
and thus the above condition becomes A < 1. Since c is the speed of propagation
of a signal or wave for the wave equation, A is the ratio of the distance such
that a signal travels in one time step to the length of a special step of the net.
Thus, if such signals cannot move more than the distance Ax in the time At,
then the numerical domain contains the analytical domain of dependence.

5.8 Numerical Dissipation and Dispersion:
Artificial Viscosity

In Chapters 11 and 12 the numerical methods for solving the Euler and Navier-
Stokes equations will be discussed. The basis for this discussion will be the
numerical methods described in Sections 5.1, 5.2, 5.3, 5.4 and 5.6 for model
equations. Since the solutions of these equations are being obtained within an