Page 211 - Computational Fluid Dynamics for Engineers

6.6 Applications of the Panel Method 199

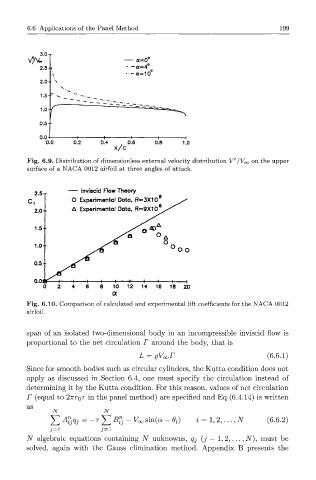
3.0
V?V~ — <x=0°
2.5 - -a=4°
-•-a=10°
2.0
1.5
•°f

0.5 +

0.0
0.0 0.2 0.4 0.6 0.8 1.0
X / C
Fig. 6.9. Distribution of dimensionless external velocity distribution V^/Ko on the upper
surface of a NACA 0012 airfoil at three angles of attack.

— Inviscid Flow Theory
2.5 T

Fig. 6.10. Comparison of calculated and experimental lift coefficients for the NACA 0012
airfoil.

span of an isolated two-dimensional body in an incompressible inviscid flow is
proportional to the net circulation r around the body, that is
L = gVoor (6.6.1)

Since for smooth bodies such as circular cylinders, the Kutta condition does not
apply as discussed in Section 6.4, one must specify the circulation instead of
determining it by the Kutta condition. For this reason, values of net circulation
r (equal to 27rror in the panel method) are specified and Eq (6.4.14) is written

N N
n
2
£ A l3q 3 = -TJ2 Z?J ~ Voo sin(a - 9 Z) i = 1, , . . . , N (6.6.2)
j=i i = i
N algebraic equations containing N unknowns, qj (j = 1,2,..., TV), must be
solved, again with the Gauss elimination method. Appendix B presents the