Page 214 - Computational Fluid Dynamics for Engineers

202 6. Inviscid Flow Equations for Incompressible Flows

+ 10° Flap

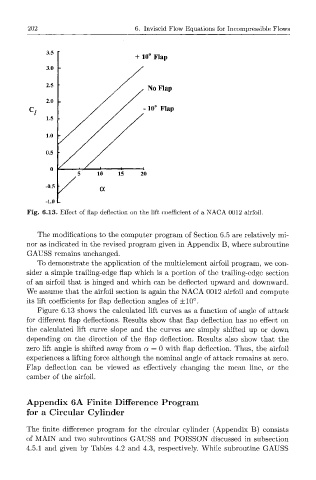
Fig. 6.13. Effect of flap deflection on the lift coefficient of a NACA 0012 airfoil.

The modifications to the computer program of Section 6.5 are relatively mi-
nor as indicated in the revised program given in Appendix B, where subroutine
GAUSS remains unchanged.
To demonstrate the application of the multielement airfoil program, we con-
sider a simple trailing-edge flap which is a portion of the trailing-edge section
of an airfoil that is hinged and which can be deflected upward and downward.
We assume that the airfoil section is again the NACA 0012 airfoil and compute
its lift coefficients for flap deflection angles of ±10°.
Figure 6.13 shows the calculated lift curves as a function of angle of attack
for different flap deflections. Results show that flap deflection has no effect on
the calculated lift curve slope and the curves are simply shifted up or down
depending on the direction of the flap deflection. Results also show that the
zero lift angle is shifted away from a = 0 with flap deflection. Thus, the airfoil
experiences a lifting force although the nominal angle of attack remains at zero.
Flap deflection can be viewed as effectively changing the mean line, or the
camber of the airfoil.

Appendix 6A Finite Difference Program
for a Circular Cylinder

The finite difference program for the circular cylinder (Appendix B) consists
of MAIN and two subroutines GAUSS and POISSON discussed in subsection
4.5.1 and given by Tables 4.2 and 4.3, respectively. While subroutine GAUSS