Page 316 - Computational Fluid Dynamics for Engineers

306 10. Inviscid Compressible Flow

-4
'
-3.5
-3 -
-2.5
#
<# -2
-1.5 ^ 1
Q_ Q_ -1 3
O / ^ O ill
-0.5 \- ^ \ -0.5 - y
oh ia 0
0.5 0 0.5
1 K=1.8 1 —e K=1.15
I
1.5 |— 1.5
. , , , i
2 i i i i I i > i i I i i i i I
0.5 0.5
x/c x/c
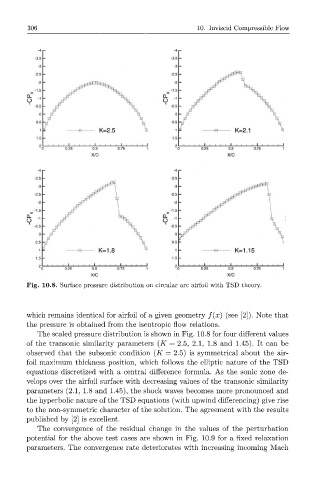
Fig. 10.8. Surface pressure distribution on circular arc airfoil with TSD theory.

which remains identical for airfoil of a given geometry f(x) (see [2]). Note that
the pressure is obtained from the isentropic flow relations.
The scaled pressure distribution is shown in Fig. 10.8 for four different values
of the transonic similarity parameters (K = 2.5, 2.1, 1.8 and 1.45). It can be
observed that the subsonic condition (K = 2.5) is symmetrical about the air-
foil maximum thickness position, which follows the elliptic nature of the TSD
equations discretized with a central difference formula. As the sonic zone de-
velops over the airfoil surface with decreasing values of the transonic similarity
parameters (2.1, 1.8 and 1.45), the shock waves becomes more pronounced and
the hyperbolic nature of the TSD equations (with upwind differencing) give rise
to the non-symmetric character of the solution. The agreement with the results
published by [2] is excellent.
The convergence of the residual change in the values of the perturbation
potential for the above test cases are shown in Fig. 10.9 for a fixed relaxation
parameters. The convergence rate deteriorates with increasing incoming Mach