Page 74 - Computational Retinal Image Analysis

4 Retinal image registration 65

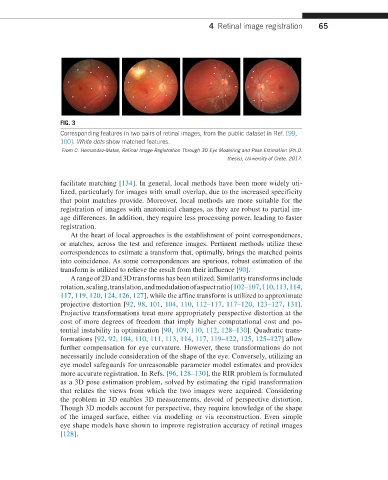
FIG. 3
Corresponding features in two pairs of retinal images, from the public dataset in Ref. [99,
100]. White dots show matched features.
From C. Hernandez-Matas, Retinal Image Registration Through 3D Eye Modelling and Pose Estimation (Ph.D.
thesis), University of Crete, 2017.

facilitate matching [134]. In general, local methods have been more widely uti-
lized, particularly for images with small overlap, due to the increased specificity
that point matches provide. Moreover, local methods are more suitable for the
registration of images with anatomical changes, as they are robust to partial im-
age differences. In addition, they require less processing power, leading to faster
registration.
At the heart of local approaches is the establishment of point correspondences,
or matches, across the test and reference images. Pertinent methods utilize these
correspondences to estimate a transform that, optimally, brings the matched points
into coincidence. As some correspondences are spurious, robust estimation of the
transform is utilized to relieve the result from their influence [90].
A range of 2D and 3D transforms has been utilized. Similarity transforms include
rotation, scaling, translation, and modulation of aspect ratio [102–107, 110, 113, 114,
117, 119, 120, 124, 126, 127], while the affine transform is utilized to approximate
projective distortion [92, 98, 101, 104, 110, 112–117, 117–120, 123–127, 131].
Projective transformations treat more appropriately perspective distortion at the
cost of more degrees of freedom that imply higher computational cost and po-
tential instability in optimization [90, 109, 110, 112, 128–130]. Quadratic trans-
formations [92, 92, 104, 110, 111, 113, 114, 117, 119–122, 125, 125–127] allow
further compensation for eye curvature. However, these transformations do not
necessarily include consideration of the shape of the eye. Conversely, utilizing an
eye model safeguards for unreasonable parameter model estimates and provides
more accurate registration. In Refs. [96, 128–130], the RIR problem is formulated
as a 3D pose estimation problem, solved by estimating the rigid transformation
that relates the views from which the two images were acquired. Considering
the problem in 3D enables 3D measurements, devoid of perspective distortion.
Though 3D models account for perspective, they require knowledge of the shape
of the imaged surface, either via modeling or via reconstruction. Even simple
eye shape models have shown to improve registration accuracy of retinal images
[128].