Page 100 - Computational Statistics Handbook with MATLAB

Chapter 4: Generating Random Variables 87

irv = irv+1
else
rej(irej) = y;
rejy(irej) = u*c; % really comparing u*c<=2*y
irej = irej + 1
end
end
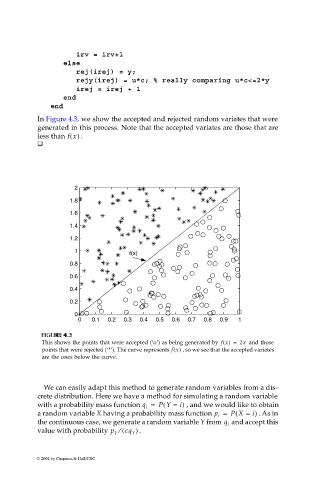
In Figure 4.3, we show the accepted and rejected random variates that were
generated in this process. Note that the accepted variates are those that are
less than f x() .

2
1.8
1.6

1.4
1.2
1 f(x)
0.8

0.6
0.4
0.2
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

F FI IG URE G 4. RE 4. 3 3
U
3
GU
F F II GU RE RE 4. 4. 3
This shows the points that were accepted (‘o’) as being generated by f x() = 2x and those
points that were rejected (‘*’). The curve represents f x() , so we see that the accepted variates
are the ones below the curve.
We can easily adapt this method to generate random variables from a dis-
crete distribution. Here we have a method for simulating a random variable
(
with a probability mass function q i = PY = i) , and we would like to obtain
(
a random variable X having a probability mass function p i = PX = i) . As in
the continuous case, we generate a random variable Y from and accept this
q i
value with probability p Y (⁄ cq Y . )

© 2002 by Chapman & Hall/CRC