Page 106 - Computational Statistics Handbook with MATLAB
P. 106
Chapter 4: Generating Random Variables 93
y = gampdf(x,t,1/lam);
bar(h,N,1,'w')
hold on
plot(x,y,'k')
hold off
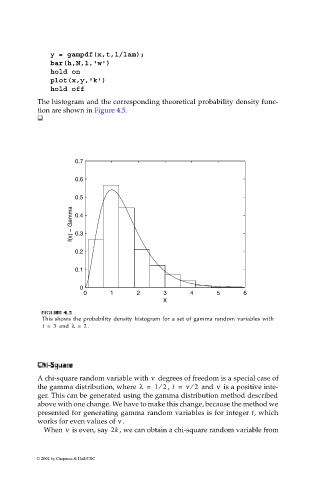
The histogram and the corresponding theoretical probability density func-
tion are shown in Figure 4.5.
0.7
0.6
0.5
f(x) − Gamma 0.4
0.3
0.2
0.1
0
0 1 2 3 4 5 6
X
IG
F FI U URE G 4. RE 4. 5 5
F F II GU RE RE 4. 4. 5
5
GU
This shows the probability density histogram for a set of gamma random variables with
t = 3 and λ = 2 .
ee
Chi- -SSquar quare e
Chi
-- SSquarquar
ChiChi
ν
A chi-square random variable with degrees of freedom is a special case of
⁄
⁄
ν
the gamma distribution, where λ = 12 , t = ν 2 and is a positive inte-
ger. This can be generated using the gamma distribution method described
above with one change. We have to make this change, because the method we
presented for generating gamma random variables is for integer t, which
ν
works for even values of .
ν
When is even, say 2k , we can obtain a chi-square random variable from
© 2002 by Chapman & Hall/CRC