Page 324 -

Section 10.1 The Hough Transform 292

of lines that passes through any point token. In particular, the lines that lie on
the curve in line space given by r = −x 0 cos θ + y 0 sin θ all pass through the point
token at (x 0 ,y 0 ).

1

0.8

0.6

0.4

0.2
0
0 0.2 0.4 0.6 0.8 1
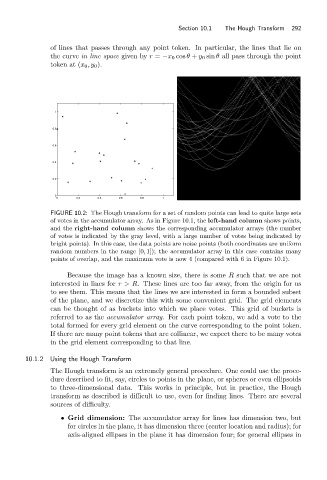
FIGURE 10.2: The Hough transform for a set of random points can lead to quite large sets
of votes in the accumulator array. As in Figure 10.1, the left-hand column shows points,
and the right-hand column shows the corresponding accumulator arrays (the number
of votes is indicated by the gray level, with a large number of votes being indicated by
bright points). In this case, the data points are noise points (both coordinates are uniform
random numbers in the range [0, 1]); the accumulator array in this case contains many
points of overlap, and the maximum vote is now 4 (compared with 6 in Figure 10.1).
Because the image has a known size, there is some R such that we are not
interested in lines for r> R. These lines are too far away, from the origin for us
to see them. This means that the lines we are interested in form a bounded subset
of the plane, and we discretize this with some convenient grid. The grid elements
can be thought of as buckets into which we place votes. This grid of buckets is
referred to as the accumulator array. For each point token, we add a vote to the
total formed for every grid element on the curve corresponding to the point token.
If there are many point tokens that are collinear, we expect there to be many votes
in the grid element corresponding to that line.

10.1.2 Using the Hough Transform

The Hough transform is an extremely general procedure. One could use the proce-
dure described to fit, say, circles to points in the plane, or spheres or even ellipsoids
to three-dimensional data. This works in principle, but in practice, the Hough
transform as described is difficult to use, even for finding lines. There are several
sources of difficulty.

• Grid dimension: The accumulator array for lines has dimension two, but
for circles in the plane, it has dimension three (center location and radius); for
axis-aligned ellipses in the plane it has dimension four; for general ellipses in