Page 424 -

392

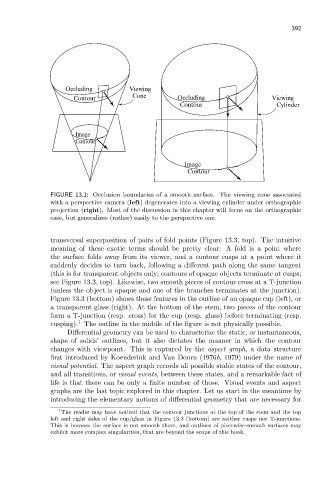
Occluding Viewing
Contour Cone Occluding Viewing
Contour Cylinder

Image
Contour

Image
Contour

FIGURE 13.1: Occlusion boundaries of a smooth surface. The viewing cone associated
with a perspective camera (left) degenerates into a viewing cylinder under orthographic
projection (right). Most of the discussion in this chapter will focus on the orthographic
case, but generalizes (rather) easily to the perspective one.

transversal superposition of pairs of fold points (Figure 13.3, top). The intuitive
meaning of these exotic terms should be pretty clear: A fold is a point where
the surface folds away from its viewer, and a contour cusps at a point where it
suddenly decides to turn back, following a different path along the same tangent
(this is for transparent objects only; contours of opaque objects terminate at cusps;
see Figure 13.3, top). Likewise, two smooth pieces of contour cross at a T-junction
(unless the object is opaque and one of the branches terminates at the junction).
Figure 13.3 (bottom) shows these features in the outline of an opaque cup (left), or
a transparent glass (right). At the bottom of the stem, two pieces of the contour
form a T-junction (resp. cross) for the cup (resp. glass) before terminating (resp.
1
cusping). The outline in the middle of the figure is not physically possible.
Differential geometry can be used to characterize the static, or instantaneous,
shape of solids’ outlines, but it also dictates the manner in which the contour
changes with viewpoint. This is captured by the aspect graph, a data structure
first introduced by Koenderink and Van Doorn (1976b, 1979) under the name of
visual potential. The aspect graph records all possible stable states of the contour,
and all transitions, or visual events, between these states, and a remarkable fact of
life is that there can be only a finite number of those. Visual events and aspect
graphs are the last topic explored in this chapter. Let us start in the meantime by
introducing the elementary notions of differential geometry that are necessary for

1 The reader may have noticed that the contour junctions at the top of the stem and the top
left and right sides of the cup/glass in Figure 13.3 (bottom) are neither cusps nor T-junctions.
This is because the surface is not smooth there, and outlines of piecewise-smooth surfaces may
exhibit more complex singularities, that are beyond the scope of this book.