Page 164 -

3.6 Geometric transformations 143

(a) (b)

(c) (d)

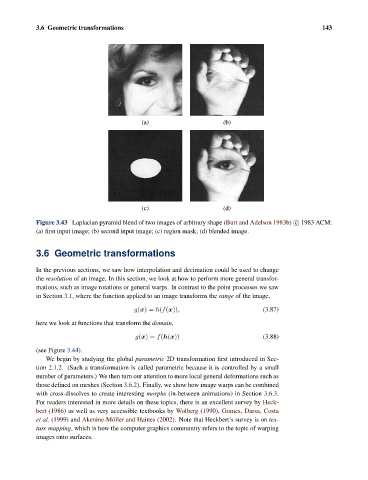
Figure 3.43 Laplacian pyramid blend of two images of arbitrary shape (Burt and Adelson 1983b) c 1983 ACM:
(a) first input image; (b) second input image; (c) region mask; (d) blended image.

3.6 Geometric transformations

In the previous sections, we saw how interpolation and decimation could be used to change
the resolution of an image. In this section, we look at how to perform more general transfor-
mations, such as image rotations or general warps. In contrast to the point processes we saw
in Section 3.1, where the function applied to an image transforms the range of the image,

g(x)= h(f(x)), (3.87)
here we look at functions that transform the domain,

g(x)= f(h(x)) (3.88)
(see Figure 3.44).
We begin by studying the global parametric 2D transformation first introduced in Sec-
tion 2.1.2. (Such a transformation is called parametric because it is controlled by a small
number of parameters.) We then turn our attention to more local general deformations such as
those defined on meshes (Section 3.6.2). Finally, we show how image warps can be combined
with cross-dissolves to create interesting morphs (in-between animations) in Section 3.6.3.
For readers interested in more details on these topics, there is an excellent survey by Heck-
bert (1986) as well as very accessible textbooks by Wolberg (1990), Gomes, Darsa, Costa
et al. (1999) and Akenine-M¨ oller and Haines (2002). Note that Heckbert’s survey is on tex-
ture mapping, which is how the computer graphics community refers to the topic of warping
images onto surfaces.